2015-03-27
271
Из приведённой типизации и схематизации получаем двумерную нестационарную математическую модель формирования качества воды, которая описывается уравнением вида
|
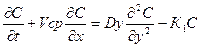
где С- концентрация загрязняющих веществ, Vcp- средняя скорость течения водного объекта, Dy- коэффициент турбулентной диффузии, К1- коэффициент неконсервативности.
Для математического решения дифференциального уравнения выбираем метод конечных разностей с граничными условиями второго рода
По явной конечно-разностной схеме выбранное дифференциальное уравнение можно представить в виде
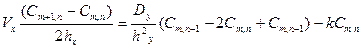(2.30)
Основные принципы:
Моделирование ведётся с постоянными характеристиками по сечению каждого участка
В направлении течения возможно задание новых гидрологических характеристик: скорости, ширины реки, коэффициентов поперечной диффузии
В случае ветвления участка реки, распределение масс загрязняющих веществ происходит пропорционально расходу воды в каждом из водотоков
Моделирование ведётся раздельно для каждого из источников загрязнения, общий результат распределения концентраций получается суммированием полей концентраций от всех водовыпусков с полем фоновых значений.
5.4.1.4. Расчётные параметры
Для математических расчетов распределения неконсервативных примесей в водотоках распределением концентрации примесей по вертикали потока пренебрегают, также не учитывается фактор времени. В данной системе за основу принято уравнение для однородной изотропной стационарной двумерной модели с учетом самоочищения:
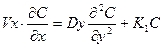(2.31)
Для расчета этого дифференциального уравнения используется дискретный метод, для чего весь участок реки разбивается на участки, исходя из условий устойчивости. Количество участков по длине и ширине участка реки определяется параметрами Mx и Ny соответственно. При выборе этих параметров должно выполняться соотношение:
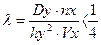, (2.32)
где hx – величина шага по длине реки (L / Mx), hy – величина шага по ширине реки (B / Ny), Dy – поперечная диффузия, Vx – скорость течения реки.
