Краткая характеристика Невской губы

Невская губа - мелководный, высокопроточный водоем с большой площадью водной поверхности. Наибольшие глубины - от 7 до 17 м - наблюдаются в северо-западной части акватории. На мелководных участках глубина колеблется от 1,5 до 5,5 м. Время пребывания воды в губе в зависимости от гидродинамических условий составляет 2-7 суток. Небольшая глубина, большая площадь водного зеркала, открытость ветрам обеспе­чивают хорошее перемешивание водной толщи по вертикали и отсутствие термической стратификации. Поэтому при моделировании биотического комплекса экосистемы этого водоема принципиально необходимо учиты­вать перенос сестона и загрязняющих веществ по акватории.

В настоящее время применяются различные модели для моделирование гидродинамических процессов и переноса пассивной примеси в Невской губе и восточной части Финского залива.

Кратко рассмотрим разработанную в институте океанологии РАН И. А. Нееловым и Д. В. Чаликовым численную трехмерную модель циркуляции жидкости в водоеме произвольной формы [28].

Модель основана на полных уравнениях гидротермодинамики жидкости: исходных уравнениях динамики вязкой несжимаемой жидкости в приближениях Буссинеска и гидростатики, уравнениях переноса тепла, соли и пассивной примеси, уравнении состояния жидкости любой степени сложности.

В модели может быть использовано любое горизонтальное и вертикальное разрешение. Модель может применяться как для диагноза, интер­поляции, усвоения данных, так и для прогноза.

Модель основана на уравнениях движения вязкой несжимаемой жидкости на сфере

В соответствии со схемой аппроксимации вся акватория Невской губы была условно разделена на 33 участка (камеры) в соответствии с рисунком 2.8. Каждая камера характеризовалась средней глубиной, площадью водного зеркала, количеством граней соприкосновения ее с другими камерами и площадью этих граней. Каждую камеру описывала своя подмодель экосистемы, в которой выделены следующие компоненты:

фитопланктон,

зоопланктон,

зообентос,

рыба,

мертвое вещество воды, находящееся на начальной стадии разложения,
совместно с разлагающими его бактериями,

мертвое вещество воды, прошедшее первую стадию разложения,
совместно с разлагающими его бактериями,

мертвое вещество дна, находящееся на начальной стадии разложения,
совместно с разлагающими его бактериями,

мертвое вещество дна, прошедшее первую стадию разложения,
совместно с разлагающими его бактериями,

биогенные вещества воды (кислород, азот, фосфор),

токсические вещества воды,

биогенные токсические вещества дна.

вещества дна (кислород, азот, фосфор),

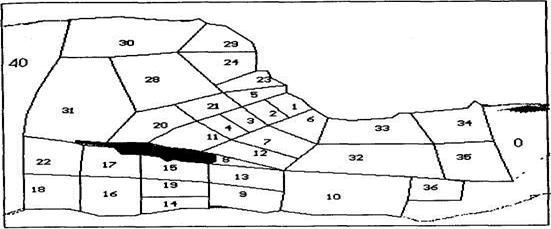
Рисунок 2.8 - схема расположения выделенных в Невской губе участков, использованная при моделировании.

Схема стоковых течений, построенная по натурным данным [29], приведена на в соответствии с рисунком 2.9. Стоковые течения, хотя их повторяемость сравнительно невелики являются постоянно действующими и определяющими вынос воды

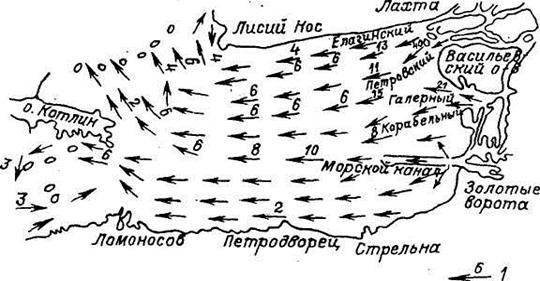
Рисунок 2.9 - схема стоковых течений в Невской губе по натурным данным

1- направление и величина скорости, м/с.

Невской губы.. Средние скорости, обусловленные стоком р. Невы, 4...6 см/с, в районе Морского канала скорости увеличиваются до 8...10 см/с. Средний многолетний расход р. Невы 2500 м3/с Колебания его сравнительно невелики. В соответствии с натурными данными в Невской губе доминирующими являются течения, формирующиеся под влиянием стока р. Невы и колебаний уровня. Ветер скоростью менее 2 м/с практически не влияет на план течений. При усилении ветра изменяется скорость потока в зонах замедленного течения у побережья; при скорости ветра более 5 м3/с влияние его на характер течения весьма существенно. Однако повторяемость ветра со средней скоростью свыше 5 m/c менее 30%. Кроме того, относительна роль ветровой составляющей в формировании течений резко падает при колебаниях уровня.

В связи с относительным постоянством скоростей и направлений векторов течения в Невской губе для ориентировочных оценок распространения загрязняющих веществ в водном объекте возможно применение моделей аналогичным речным системам.

5.7.2. Моделирование прибрежных зон Финского залива (Краткое описание модели экосистемы Финского залива) [26]

Система моделей на вложенных сетках работает следующим образом. Сначала на двумерной модели «мелкой воды» всего Балтийского моря рассчитываются изменения уровня моря на входе в Финский залив. С этими граничными условиями трехмерная гидродинамическая модель вос­производит циркуляцию вод в Финском заливе на пятимильной сеточной области с временным шагом в три часа. Вертикальная структура аппроксимирована девятью слоями с верхними границами, расположенными на глубинах 0, 3, 5, 10, 15, 20, 30, 50, и 60 м. И, наконец, горизонтальные и вертикальные потоки воды интегрируются в пределах каждых суток в соответствие с трехмерной структурой боксовой модели представлено на рисунке 2.10, воспроизводящей взаимодействие процессов физического переноса и биогеохимических превращений в каждом «столбце» боксов на одномерной модели вертикальной диффузии неконсервативных субстанций - экосистемных переменных модели. В водной толще такими переменными являются: сообщества автотрофов и гетероторофов, органические азот и фосфор, содержащиеся в детрите, аммоний, нитраты и фосфаты, а также растворенный кислород. Придонные боксы взаимодействуют также с лабильными соединениями азота и фосфора, содержащимися в верхнем активном слое донных отложений.

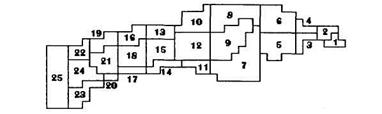
Рисунок 2.10 - Боксовая аппроксимация Финского залива в модели

Боксы примерно соответствуют: 1 - Невской Губе, 2 - мелководному району, 3 и 4 - переход­ному району, 5 и 6 - внешнему эстуарию Невы, 7 - Нарвскому заливу, 8 - финским шхерам, 9 - открытым водам восточной части Финского залива

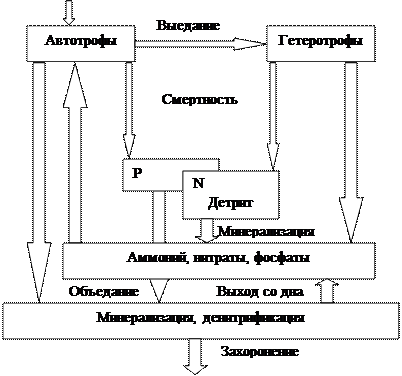Рисунок 2.11- обобщенная схема биогеохимических потоков вещества в модели

Список литературы

1. Абакумов В. А. (ред.) Руководство по методам гидробиологического анализа поверхностных вод и донных отложений. Л.: Гидрометеоиздат, 1983.

2. Руководство по химическому анализу вод суши Л., Гидрометеоиздат, 1977

3.Шишкин А.И. Математическое моделирование переноса примесей и прогнозирование состава окружающей среды. – Л.: Ленинградская лесотехническая академия, 1981. – 123 с.

4. Экология: Учебник для технических вузов / Л.И. Цветкова, М.И. Алексеев и др.; под ред. Л.И. Цветковой. –М.: Изд-во АСВ, СПб.: Химиздат, 2001. – 552 с.

5.. Дружинин Н.И., Шишкин А.И. Математическое моделирование и прогнозирование загрязнения поверхностных вод суши. – Л.: Гидрометеоиздат, 1989. – 329 с.

6. Шишкин А.И., Жуков К.Г., Саяпин К.Я. Вычислительные средства систем управления качество окружающей среды. – Л.: Ленинградская лесотехническая академия, 1986. – 88 с.

7. Афанасьев А.И. Оптимизация предельно допустимого сброса промстоков ЦБП методами машинного моделирования при проектировании систем водоотведения: Автореф… канд. техн. наук. – Л.: Технологический институт целлюлозно-бумажной промышленности, 1988. – 16 с.

8. Дружинин Н.И., Шишкин А.И. Метод электро-конвективно-диффузионной аналогии и его применение при составлении прогноза качества воды в водоёмах. – М.: ВДНХ, 1975. – 34 с.

9. Вавилин В.А., Циткин А.И. Математическое моделирование качества воды // Водные ресурсы. – 1977. – № 5. – С. 114–133

10. Беки Дж.А., Карплюс У.Дж. Теория и применение гибридных вычислительных систем. – М.: Мир, 1970. – 483 с.

11. Кюнж Ж.А. и др. Численные методы в задачах речной гидравлики: практическое применение / Ж.А. Кюнж, Ф.М. Холли, А. Вервей – М.: Энергоиздат, 1985. – 256 с.

12. Рихтмайер Р., Мортон К. Разностные методы решения краевых задач. – М.: Мир, 1972. – 418 с

13. Жуков К.Г., Подобед М.В. Модификационный метод Эйлера и его реализация средствами АЦВТ // Расширенное заседание Национального комитета Международной ассоциации по аналоговым вычислениям: Тр. – Рязань, 1978. – С. 38–42.

14. Рихтмайер Р., Мортон К. Разностные методы решения краевых задач. – М.: Мир, 1972. – 418 с.

15. Лапшев Н.Н. Расчёты выпусков сточных вод/ Н.Н. Лапшев. – М.: Стройиздат, 1977, -87 с

16. Шишкин А.И. Основы математического моделирования конвективно-диффузионного переноса примесей. – Л.: ЛТИ ЦБП, 1976. – 243 с.

17. Афанасьев А.И. Оптимизация предельно допустимого сброса промстоков ЦБП методами машинного моделирования при проектировании систем водоотведения: Автореф… канд. техн. наук. – Л.: Технологический институт целлюлозно-бумажной промышленности, 1988. – 16 с

18. Жуков К.Г., Лоренц Е.А. Специализированный аналоговый процессор на линейных интегральных схемах. Линейные интегральные схемы и их применение в приборостроении и промышленной автоматике // Всесоюзная научно-техническая конференция. – Л.: ЛЭТИ, 1977

19. Шишкин А.И. К вопросу теории развития метода ЭКДА и практики его применения при прогнозе качества воды // Материалы VI Всесоюзного симпозиума по современным проблемам самоочищения водоёмов и регулирования качества воды. – Секция 1. – Таллин: ТПИ, 1979. – С. 23–35

20. Флетчер К. Вычислительные методы в динамике жидкостей: Пер. с англ. – М.: Мир, 1991. – Т.1. – 504 с

21. Гультяев А. Имитационное моделирование в среде Windows. – СПб: Корона принт, 1999. – 288 с

22. Гультяев А. Визуальное моделирование в среде MatLab: учебный курс. – CПб: Питер, 2000. – 432 с.

23. Математическое моделирование природных экосистем / В.И. Косов, Д.Ф. Шульгин, В.Е. Клыков, В.Н. Иванов. – Тверь, 1998. – 255 с

24. Гультяев А. Визуальное моделирование в среде MatLab: учебный курс. – CПб: Питер, 2000. – 432 с.

25. Горбунов Н.Е., Шишкин А.И. Имитационное моделирование задач прогноза качества воды аналого-цифровыми средствами // Научно-технические ведомости СПбГТУ. – СПБ: Изд-во СПбГТУ, 2000. - №4. - C. 122-130

26. Марчук Г.И. Математическое моделирование в проблеме окружающей среды. – М.: Наука, 1982. – 320 с.

27. Караушев А.В., Речная гидравлика, Л. Гидрометиоиздат, 1969, 416 с

28. Интегрированное управление водными ресурсами Санкт- Петербурга и Ленинградской области/ опыт создания систем поддержки принятия решений. СПб.: Borey Print, 2001, 419c.

29 Маневич Я.З.; Обоснование основных параметровгенеральной гидравлической модели Невской губы, Известия issn 0368-0738

30. Гиргидов А. Д. Турбулентная диффузия с конечной скоростью.— СПб.: Изд-во СПбГТУ, 1996.— 259с.

31.Гиргидов А. Д. Техническая механика жидкости и газа (одномерные задачи): Учеб. пособие / А. Д. Гиргидов; ЛГТУ.—Л.: ЛГТУ, 1990.—79 с.

32. Основы прогнозирования качества поверхностных вод. – М.: Наука, 1982, - 181 с

33. Черкинский С.Н. Санитарные условия спуска сточных вод в водоёмы. – М.: Стройиздат, 1977. – 224 с.

34. Лапшев Н.Н. Расчёты выпусков сточных вод/ Н.Н. Лапшев. – М.: Стройиздат, 1977, -87 с

35. Шишкин А.И. Определение допустимых промышленных выбросов ЦБП в водоёмы методом ЭКДА. – Л.: Ленинградская лесотехническая академия, 1983. – 50 с.

36. Юделевич А.М. Идентификация параметров моделей фильтрационного режима в системе «Гравитационная бетонная плотина – скальное основание»: Автореф… канд. техн. наук. – СПб, 1999. – 25 с

37. Беличенко Ю.П., Карабан И.Н., Косовцева Л.В. Об одном подходе к расчёту предельно допустимых сбросов в водные объекты // География и природные ресурсы. – 1986. – №2. – С. 119–122.

38. Ревская губа, опыт моделирования; издание Санкт-Петербуржского научного центра,; под редакцией Нищенко1957г, 419 с

39. рх. ГГИ, №43348, 1981 год

40. Нижеховский Р.А.; Вопросы гидрологии реки Невы и Невской губы, Л. гидромететеоиздат, 1988 г

41. Нижеховский Р.А. Вопросы формирования качества вод реки Невы и Невской губы; Л. гидрометеоиздат. 1985 г

42. Зимин А.А, Белоусова Н.В.; Гидрохимический словарь, Л. гидрометиоиздат, 1988 г.