В общем виде выше было получено уравнение переноса (16):
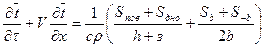
В системе с краевыми условиями (17)-(19) уравнение может решаться численным методом совместно с уравнениями движения и неразрывности или отдельно, когда известны значения 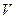 и
и 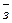 . Кроме того, при достаточно малой скорости
. Кроме того, при достаточно малой скорости 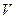 или её отсутствии уравнение (13) позволяет рассчитать термический режим водоёма с учётом колебаний уровня относительно некоторой глубины по заданным величинам
или её отсутствии уравнение (13) позволяет рассчитать термический режим водоёма с учётом колебаний уровня относительно некоторой глубины по заданным величинам 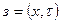 .
.
Величина теплового потока через верхнюю поверхность водотока 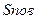 определяется в основном приходом тепла солнечной радиации
определяется в основном приходом тепла солнечной радиации 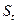 , конвективным теплообменом
, конвективным теплообменом 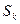 , величиной теплоотдачи испарением
, величиной теплоотдачи испарением 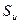 , а также наличием льда (см. рис. 3).
, а также наличием льда (см. рис. 3).
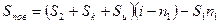 (62)
(62)
где 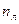 - сплочённость льда.
- сплочённость льда.
Расчёт этих составляющих может выполняться по различным методическим указаниям (например {2}).
Количества тепла 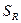 , поступающее к водной поверхности выделенного участка, определённое по радиационному балансу этой поверхности, записывается в следующем виде:
, поступающее к водной поверхности выделенного участка, определённое по радиационному балансу этой поверхности, записывается в следующем виде:
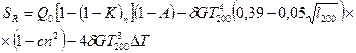 (63)
(63)
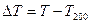 (64)
(64)
Где 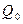 - суммарная солнечная радиация при безоблачном небе;
- суммарная солнечная радиация при безоблачном небе;
K - -коэффициент, выражающий отношение действительной радиации при сплошной облачности к возможной; 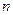 - общая облачность в десятых долях;
- общая облачность в десятых долях; 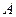 – альбедо;
– альбедо; 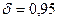 - коэффициент, учитывающий излучение тепла водной поверхностью;
- коэффициент, учитывающий излучение тепла водной поверхностью;
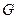 - постоянная Стефана-Больцмана;
- постоянная Стефана-Больцмана; 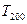 и
и 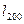 - абсолютная температура и влажность воздуха на высоте 2м;
- абсолютная температура и влажность воздуха на высоте 2м; 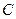 - коэффициент характеризующий влияние облаков на эффективное излучение;
- коэффициент характеризующий влияние облаков на эффективное излучение; 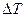 - разность абсолютных температур поверхности воды и воздуха.
- разность абсолютных температур поверхности воды и воздуха.
Для расчёта конвективного теплообмена между водной поверхностью и воздухом используется формула А.П. Браславского:
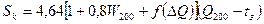 (65)
(65)
а для расчета количества' тепла, затрачиваемого на испарение воды, формула
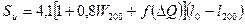 (66)
(66)
где 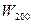 - скорость ветра;
- скорость ветра; 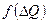 - параметр, учитывающая разность температуры поверхности воды и воздуха
- параметр, учитывающая разность температуры поверхности воды и воздуха 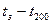 ;
; 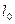 - максимальная упругость водяного пара, вычисленная по температуре испаряющая поверхности.
- максимальная упругость водяного пара, вычисленная по температуре испаряющая поверхности.
Значение скорости ветра на высоте 2м над водной поверхностью 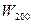 определяется по показаниям флюгера, установленного на берегу, по формуле
определяется по показаниям флюгера, установленного на берегу, по формуле
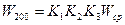 (67)
(67)
Где 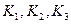 - коэффициенты, учитывающие степень защищённости станции на суше, характеристику рельефа в пункте наблюдений и среднюю длину разгона воздушного потока над водоёмом.
- коэффициенты, учитывающие степень защищённости станции на суше, характеристику рельефа в пункте наблюдений и среднюю длину разгона воздушного потока над водоёмом.
Расчёт температуры 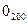 и влажности воздух
и влажности воздух 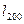 на высоте 2м над водной поверхностью по данным измерений этих параметров на суше выполняется по рекомендациям К.Н. Клибашева и И.Ф. Горошкова
на высоте 2м над водной поверхностью по данным измерений этих параметров на суше выполняется по рекомендациям К.Н. Клибашева и И.Ф. Горошкова
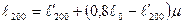 (68)
(68)
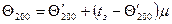
Где 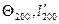 - температура и влажность воздуха на суше на высоте 2м;
- температура и влажность воздуха на суше на высоте 2м; 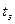 ,
, 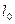 - температура поверхности воды и максимальная упругость водяного пара при этой температуре;
- температура поверхности воды и максимальная упругость водяного пара при этой температуре; 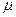 - коэффициент трансформации, учитывающий среднее изменение влажности и температуры воздуха в зависимости от размера водоёма.
- коэффициент трансформации, учитывающий среднее изменение влажности и температуры воздуха в зависимости от размера водоёма.
Теплообмен с атмосферой за счёт ледообразования:

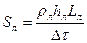 (70)
(70)
где 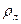 - плотность льда;
- плотность льда; 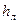 - высота льда;
- высота льда; 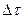 - время, ч;
- время, ч; 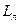 - теплота кристаллизации.
- теплота кристаллизации.
Учитывая равенство (15), в уравнениях (63)-(69) в качестве температуры поверхности воды используется средняя температура по сечению водотока.
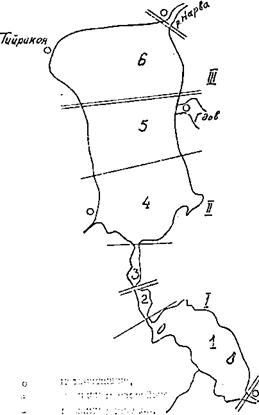
Целью расчёта по рассмотренной схеме является определение средних месячных или декадных температур воды для тёплого периода года для расчётных участков, на которые может быть разбит по длине водоток. Разбивка на участки производилась с учётом однородности гидрологических условий и с таким расчётом, чтобы данные ближайшей метеостанции можно было распространить на весь участок. На рис. 9 приведена схема разбивки Чудско-Псковского озера.
 Псков
Псков
Рис. 9. Схема Чудско-Псковского озера.
За начальные условия принимаются температуры воды для первого расчётного интервала для всех участков реки.
Граничными условиями являются средние за интервал времени температуры воды на верхней границе первого участка для всех расчётных интервалов.
Колебания уровня 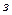 по участкам акватории губы для периода отсутствия ледостава назначаются по данным гидрологических обзоров или принимаются равными нулю, а скорости движения воды расчётным путём или по литературным источникам.
по участкам акватории губы для периода отсутствия ледостава назначаются по данным гидрологических обзоров или принимаются равными нулю, а скорости движения воды расчётным путём или по литературным источникам.
Приведённая постановка задачи позволяет проводить численные эксперименты для трёх случаев.
I вариант: 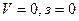 .
.
Этот вариант соответствует условиям непроточного водоёма, в котором отсутствуют колебания уровня. Изменение теплосодержания водоёма обусловлено теплообменом с окружающей средой.
Тогда из уравнения (16) получаем:
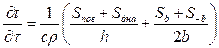
(71)
Соответственно, схема (31) принимает вид
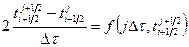
II вариант: 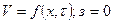
Этот вариант соответствует условиям проточного водоёма, колебания уровня в котором пренебрежимо малы.
Тогда из уравнения (16) получаем
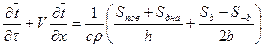 (72)
(72)
III вариант: 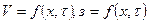
Третий вариант соответствует условиям проточного водоёма, при наличии колебаний уровня. Расчётное уравнение имеет вид (16).
Во втором и третьем случаях изменение теплосодержания водотока обусловлено теплообменом с окружающей средой, а также переносом тепла, движущимся потоком воды.
Решение задачи может быть осуществлено с помощью ЭВМ.
Алгоритм расчёта следующий. Задаваясь температурой воды 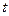 , просчитывают левая и правая части выражений (16), (71) или (72), затем они сравниваются. Допустимой считается разница, которая соответствует расхождению расчётных температур воды на
, просчитывают левая и правая части выражений (16), (71) или (72), затем они сравниваются. Допустимой считается разница, которая соответствует расхождению расчётных температур воды на 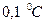 .
.
 2015-03-27
2015-03-27 633
633








