Метод логарифмического дифференцирования удобен для нахождения производной показательной функции 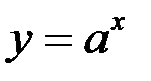 , показательно – степенной функции
, показательно – степенной функции 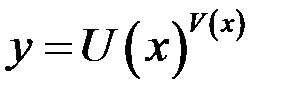 , а также, если функция представляет собой выражение вида
, а также, если функция представляет собой выражение вида 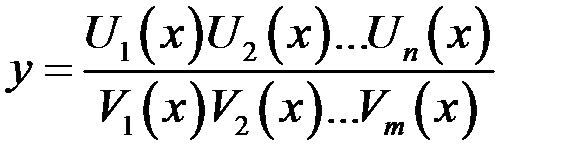 . Этот метод состоит в следующем: данное выражение сначала логарифмируют по основанию е, а затем дифференцируют как тождество, получая уравнение для нахождения производной.
. Этот метод состоит в следующем: данное выражение сначала логарифмируют по основанию е, а затем дифференцируют как тождество, получая уравнение для нахождения производной.
Пример
Найти производную функции 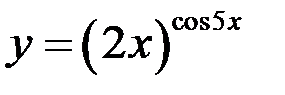 применяя метод логарифмического дифференцирования.
применяя метод логарифмического дифференцирования.
Решение
Здесь основание и показатель степени зависит от х. Логарифмируем обе части равенства 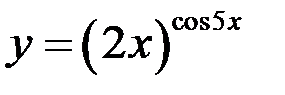 по основанию е:
по основанию е:
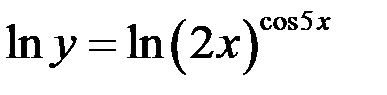 ,
,
применяя свойства логарифмов, получим
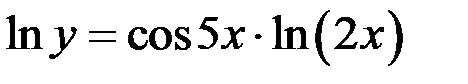 .
.
Продифференцируем обе части последнего равенства по х, рассматривая у как функцию х:
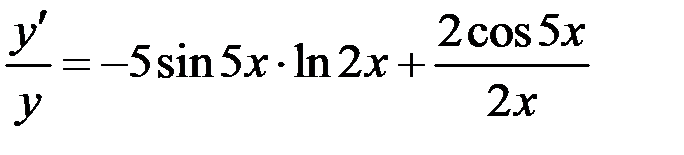 ,
,
умножим обе части равенства на у и подставим вместо у его выражение 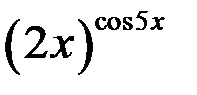 , получим
, получим
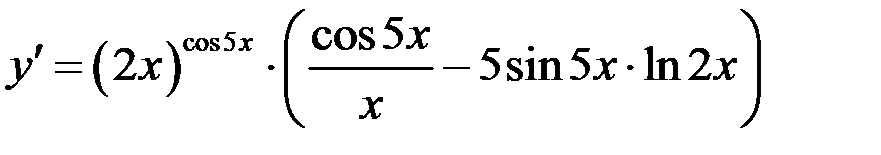 .
.
 2015-03-07
2015-03-07 6126
6126








