Пусть дана сложная функция 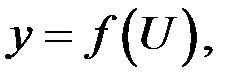 где
где 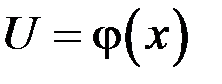 или
или 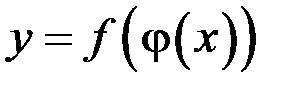 .
.
Теорема. Если функция 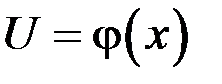 дифференцируема в точке
дифференцируема в точке 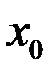 , а функция
, а функция 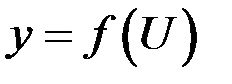 дифференцируема в точке
дифференцируема в точке 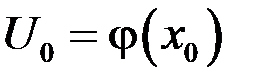 , тогда сложная функция
, тогда сложная функция 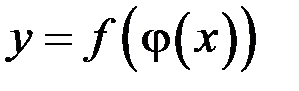 дифференцируема в точке
дифференцируема в точке 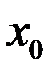 , причем
, причем
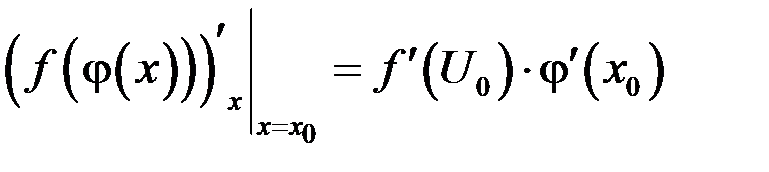 или
или 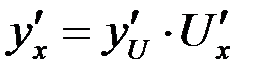
Замечание. Теорема может быть обобщена на случай любой конечной цепочки функций. Так, если 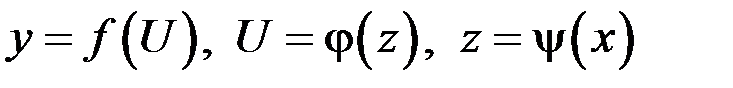 , или
, или 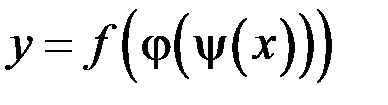 и существуют производные
и существуют производные 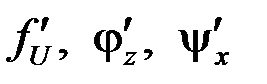 , то
, то 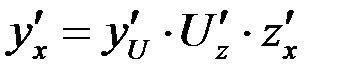 .
.
Пример
Найти производную функции 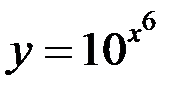 .
.
Решение
Здесь 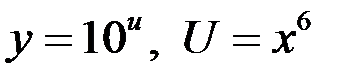 ,
,
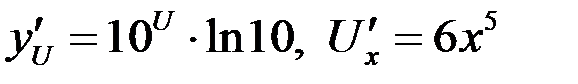 , тогда
, тогда 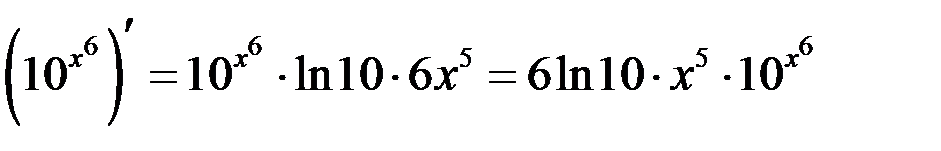 .
.
 2015-03-07
2015-03-07 546
546








