Дифференцирование функций, заданных неявно, опирается на возможность почленного дифференцирования тождеств.
В общем случае уравнение почленно дифференцировать нельзя.
Пусть функция 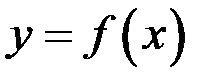 задана неявно уравнением
задана неявно уравнением 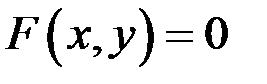 и известно, что существует решение этого уравнения в виде
и известно, что существует решение этого уравнения в виде 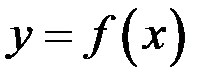 ; подставив это решение в уравнение, получим тождество
; подставив это решение в уравнение, получим тождество 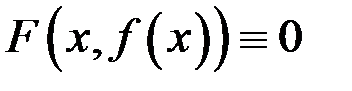 .
.
Продифференцировав 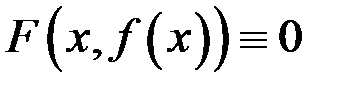 по х, получим уравнение для нахождения производной
по х, получим уравнение для нахождения производной 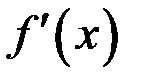 .
.
Пример
Найти производную функции, заданной неявно: 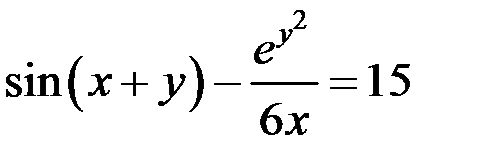 .
.
Решение
Продифференцируем обе части данного уравнения по аргументу х:
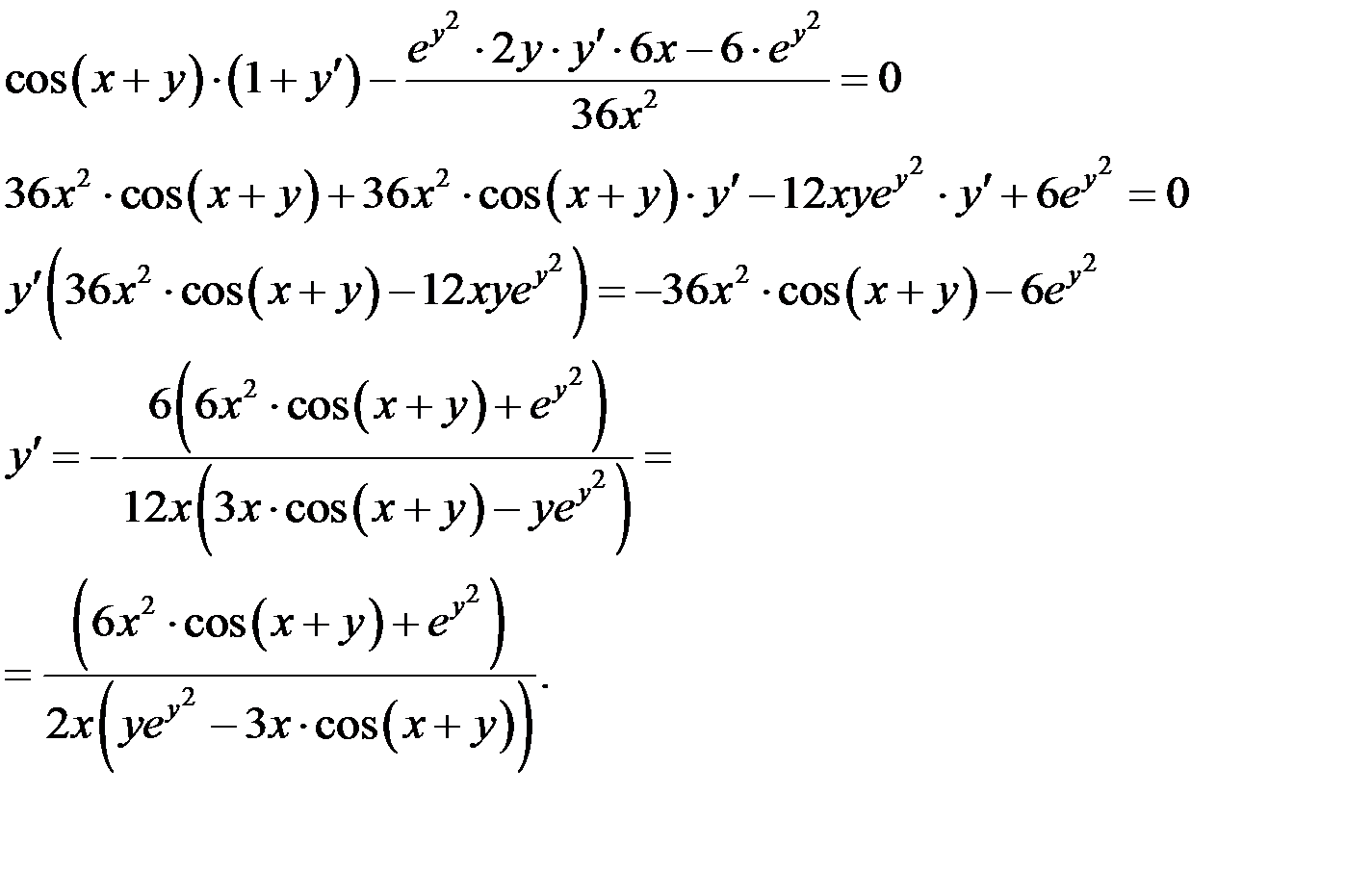
 2015-03-07
2015-03-07 1098
1098








