Примеры решения задач. Решение. Предварительно преобразуем подынтегральную функцию, вводя степени с дробными и отрицательными показателями по формулам

Задача 5. Найти интеграл: .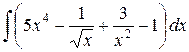

Решение. Предварительно преобразуем подынтегральную функцию, вводя степени с дробными и отрицательными показателями по формулам

, .

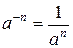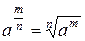Затем используем свойства 4, 3, а также табличный интеграл (1)

= =

= = =

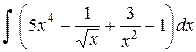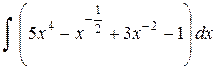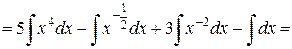
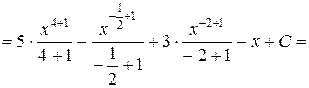
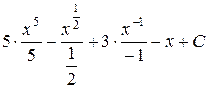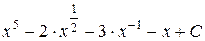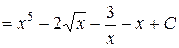
Задача 6. Найти интеграл: .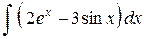

Решение. Применяя свойства 4, 3 и табличные интегралы (3), (4), имеем

.

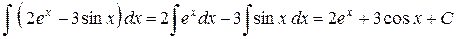Задача 7. Найти интеграл: .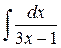

Решение. Пусть t = 3 x – 1, тогда 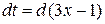или 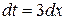, откуда 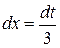. Выполним замену в подынтегральном выражении

.

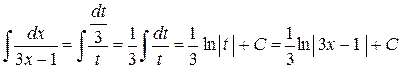Вопросы для самопроверки

1. Какая функция называется первообразной для данной функции?

2. Дайте определение неопределенного интеграла от данной функции.

3. Сформулируйте основные свойства неопределенного интеграла.