2015-03-07
277
Функциональной зависимостью называется такая взаимосвязь одной или нескольких независимых переменных величин с некоторой, зависимой от них, переменной величиной, при которой каждому значению независимых переменных соответствует строго определенное значение этой зависимой переменной.
Математическое выражение, устанавливающее вид взаимосвязи зависимой переменной с независимой, называется функцией и обозначается строчной латинской буквой f. Независимая переменная называется аргументом функции, и, как правило, обозначается строчной латинской буквой х, а зависимая переменная – у.
Например,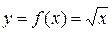 
. Здесь функцией является выражение 
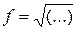. Если 
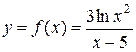, то функция имеет вид 
.
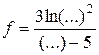Производной функции называется выражение, характеризующее быстроту изменения функции при изменении ее аргумента. Например, если мы имеем функцию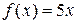 
, то, очевидно, быстрота ее изменения равна 5, то есть изменение аргумента на единицу приводит к изменению значения функции на 5 единиц. (
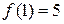, а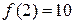 
).
В общем случае производная функции определяется как предел отношения приращения функции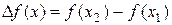 
к приращениюее аргумента 
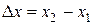. Очевидно, что если 
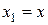, то 
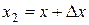, и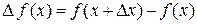 
.
|
|
|
Производная функции обозначается штрихом около символа функции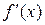 
. Таким образом, согласно определению
.
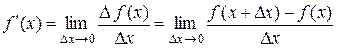Рассмотрим например нахождение производной степенной функции.
Пусть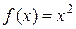 
. Тогда, согласно определению,
.
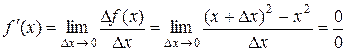Для устранения неопределенности раскроем скобки в числителе
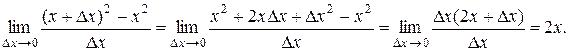
Отсюда следует общая формула производной степенной функции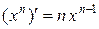 
. Нахождение производной функции называется дифференцированием.
