Источники повторных вызовов иллюстрируются с помощью модели, показанной на седьмом рисунке. Между абонентом "А" и абонентом "В" показана схема установления соединения через две АТС и два транзитных узла.
Рисунок 7
Вероятность установления соединения равна 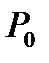 . Следовательно, доля неудачных попыток абонента "А" может оцениваться вероятностью
. Следовательно, доля неудачных попыток абонента "А" может оцениваться вероятностью 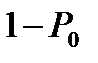 . Причины повторных попыток вызова объясняются потерями (в процессе установления соединения), занятостью абонента "В" или отсутствием ответа. Характеристики "повторения" попыток установления соединения в значительной мере определяются психологическими факторами. Наличие повторных попыток искажает ряд классических представлений о функционировании сети телефонной связи. Измерения показали, что величина потерь вызовов в несколько раз может превосходить уровень, определяемый по формуле Эрланга.
. Причины повторных попыток вызова объясняются потерями (в процессе установления соединения), занятостью абонента "В" или отсутствием ответа. Характеристики "повторения" попыток установления соединения в значительной мере определяются психологическими факторами. Наличие повторных попыток искажает ряд классических представлений о функционировании сети телефонной связи. Измерения показали, что величина потерь вызовов в несколько раз может превосходить уровень, определяемый по формуле Эрланга.
Одна из проблем анализа повторных попыток – сложность разделения первичных и вторичных вызовов. На восьмом рисунке показана соответствующая модель с указанием точек, в которых целесообразно производить измерения: X и Y. На самом деле для измерений обычно доступна только точка Z.
Рисунок 8
В первой таблице представлены данные измерений отношения успешных попыток к безуспешным для УАТС, ГТС и АМТС.
Таблица 1
| Исход попытки | Отношение успешных попыток к безуспешным | ||
| УАТС | ГТС | АМТС | |
| Успешная | 0,57 | 0,44 | 0,25 |
| Безуспешная: | 0,43 | 0,56 | 0,75 |
| блокировка | 0,04 | 0,29 | 0,56 |
| ошибка набора | 0,02 | 0,06 | 0,06 |
| абонент занят | 0,26 | 0,14 | 0,10 |
| нет ответа | 0,11 | 0,07 | 0,03 |
Поведение абонента может характеризоваться функцией настойчивости, которая определяется распределением вероятности для 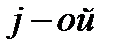 попытки. Одна из таких моделей – абсолютно настойчивый абонент, который продолжает попытки до бесконечности. Тогда при вероятности неуспешного установления соединения –
попытки. Одна из таких моделей – абсолютно настойчивый абонент, который продолжает попытки до бесконечности. Тогда при вероятности неуспешного установления соединения – 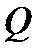 на каждой из
на каждой из 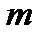 фаз обслуживания отношение интенсивности суммарного потока вызовов к интенсивности потока первичных вызовов определяется так:
фаз обслуживания отношение интенсивности суммарного потока вызовов к интенсивности потока первичных вызовов определяется так:
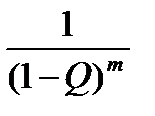 . (5)
. (5)
Для расчета СМО с повторными вызовами разработано множество моделей и методов, ориентированных на использование таблиц и/или программных продуктов. Для простых моделей получены аналитические выражения, позволяющие анализировать ряд СМО.
Полнодоступный пучок. Система с потерями.
Многофазные СМО и сети массового обслуживания
Допущения для СМО вида 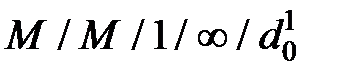 :
:
Распределение промежутков между заявками (вызовами) для первой СМО подчиняется экспоненциальному закону:
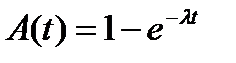 . (1)
. (1)
Распределение длительности обслуживания вызовов для всех СМО подчиняется экспоненциальному закону:
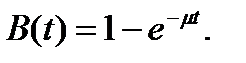 (2)
(2)
Средние значения интервалов между вызовами и времени обслуживания определяется так:
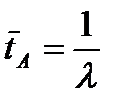 ,
, 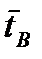 =
= 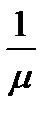 . (3)
. (3)
Условие стационарности каждой СМО:
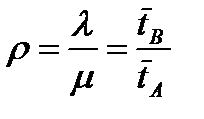
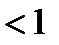 . (4)
. (4)
Сети массового обслуживания (СеМО)
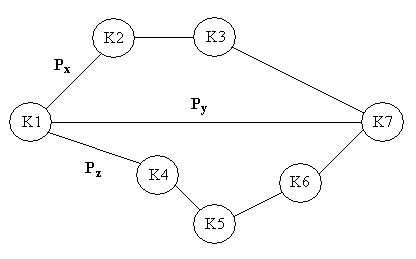
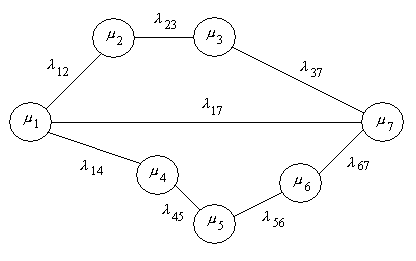
Рассмотрим модель гипотетической сети, в которой установлено семь коммутаторов (К). Нас интересует процесс обмена информацией между К1 и К7. Между этими коммутаторами установлено три пути обмена пакетами, вероятность использования которых определяется величинами 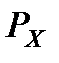 ,
, 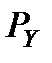 и
и 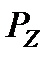 . Очевидно, сумма этих вероятностей равна единице.
. Очевидно, сумма этих вероятностей равна единице.
Допустим, что каждый коммутатор может быть представлен системой телетрафика с ожиданием. Интенсивность обработки пакета равна 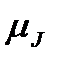 , а интенсивность входящего потока –
, а интенсивность входящего потока – 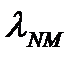 .
. 
Допустим, что каждый коммутатор может быть представлен системой телетрафика вида 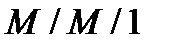 . Тогда время пребывания пакета в
. Тогда время пребывания пакета в  коммутаторе определяется по такой формуле:
коммутаторе определяется по такой формуле:
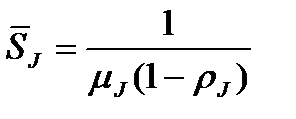 . (5)
. (5)
Загрузка определяется отношением интенсивности входящего потока к интенсивности обслуживания. Например,
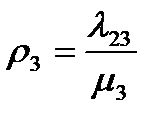 . (6)
. (6)
Средняя задержка пакета на маршруте, выбираемом с вероятность 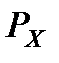 , будет определяться так:
, будет определяться так:
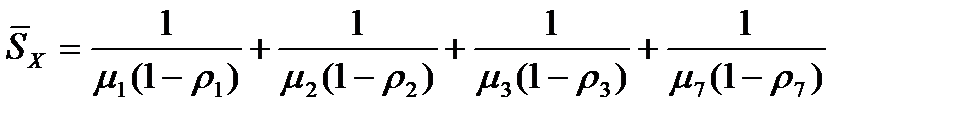 . (7)
. (7)
Средняя задержка пакета в сети массового обслуживания (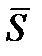 ) может оцениваться с учетом вероятностей PX, PY и PZ:
) может оцениваться с учетом вероятностей PX, PY и PZ:
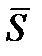 =
= 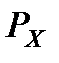
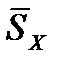 +
+ 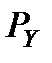
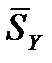 +
+ 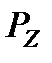
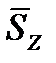 . (8)
. (8)
Вычисление квантилей функции распределения длительности задержки пакетов существенно сложнее. Обычно для их расчета используют методы имитационного моделирования.
Многофазные системы массового обслуживания
В сети массового обслуживания можно выделить многофазные СМО, для которых осуществляется оценка показателей качества обслуживания трафика – задержки и/или потери заявок. Для произвольной структуры сети пример многофазной СМО можно представить такой совокупностью таких элементов:
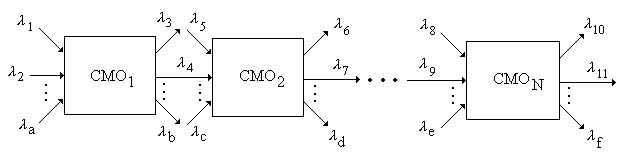
Для такой модели можно вычислить все интенсивности потоков заявок. Обычно для многофазных СМО определяются такие характеристики:
· вероятность потери заявок;
· среднее значение времени задержки заявок;
· функция распределения длительности задержки заявок.
Для алгоритма обслуживания заявок с потерями можно использовать приближенную формулу, если вероятность блокировки на каждой фазе весьма мала:
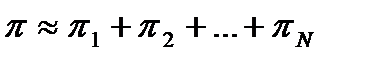 . (9)
. (9)
Для среднего времени задержки заявок действует правило аддитивности математического ожидания:
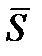 =
= 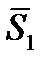 +
+ 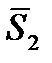 + … +
+ … + 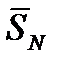 . (10)
. (10)
Для функции распределения времени задержки заявок необходимо найти свертку таких же функций, определенных для каждой СМО. Преобразование Лапласа-Стилтьеса вычисляется проще:
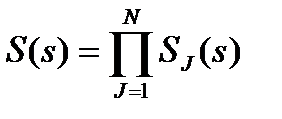 . (11)
. (11)
Сложные СМО
1. СМО вида 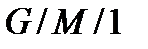
Вероятности состояний (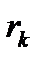 ) определяются следующим образом:
) определяются следующим образом:
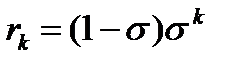 , (12)
, (12)
где  – единственное решение уравнения
– единственное решение уравнения
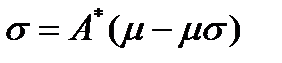 (13)
(13)
в области 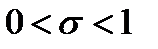 .
.
Распределение длительности ожидания для рассматриваемого класса СМО также определяется через переменную  :
:
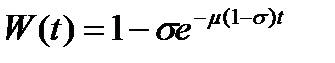 . (14)
. (14)
Средняя длительность ожидания начала обслуживания рассчитывается так:
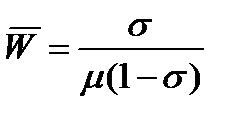 (15)
(15)
Для СМО вида 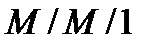 уравнение (13), учитывая, что
уравнение (13), учитывая, что 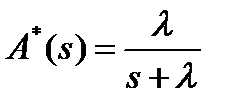 , принимает такой вид:
, принимает такой вид:
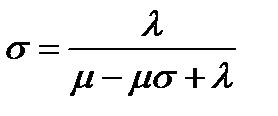
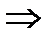 (
(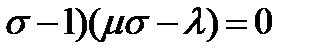 . (16)
. (16)
В уравнении (16) интересен только один корень в силу сформулированных ограничений – 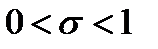 . Поэтому
. Поэтому 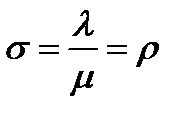 .
.
2. СМО вида 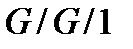
Среднее время ожидания начала обслуживания определяется следующим образом:
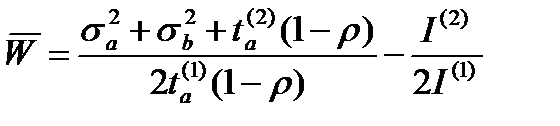 . (17)
. (17)
В этой формуле используются такие оценки:
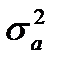 – дисперсия промежутков времени между заявками, поступающими в СМО;
– дисперсия промежутков времени между заявками, поступающими в СМО;
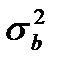 – дисперсия времени обслуживания заявок в СМО;
– дисперсия времени обслуживания заявок в СМО;
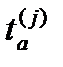 –
– 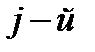 момент для времени между соседними заявками (процесс
момент для времени между соседними заявками (процесс 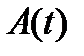 );
);
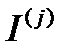 –
– 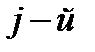 момент для длительности периода свободного состояния СМО (система, если она работоспособна) находится в двух состояниях: занятости и свободности.
момент для длительности периода свободного состояния СМО (система, если она работоспособна) находится в двух состояниях: занятости и свободности.
3. Другие сложные СМО
Другие сложные СМО могу быть представлены такими примерами:
· СМО вида 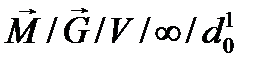
· ненадежный обслуживающий прибор;
· приоритетное обслуживание (разные алгоритмы);
· системы с обратной связью.
Преобразование модели многофазной системы
Модель СеМО, предназначенная для анализа IP сети
Модель процесса обмена IP-пакетами в сети NGN
Полнодоступный пучок. Система с повторными вызовами
Аспекты измерения трафика
1. Измерения трафика проводятся с целью решения ряда практических и теоретических задач:
· проектирование сетей электросвязи;
· управление сетями электросвязи;
· прогнозирование нагрузки;
· заключение соглашений SLA;
· проверка гипотез о количественных и качественных свойствах нагрузки;
· другие задачи.
2. Для организации процесса измерений трафика (с учетом конкретной цели измерения) необходимо выбрать:
· объект (или совокупность объектов) измерения;
· длительность периода измерения;
· микроструктуру периода измерения;
· вид и объем собираемых данных;
· величину допустимой ошибки;
· другие атрибуты.
3. Объектами измерений, которые выбраны для решения задачи, могут быть:
· общее количество поступающих вызовов;
· численность вызовов от конкретных источников трафика;
· доля состоявшихся разговоров;
· длительность обслуживания вызовов;
· задержки и потери вызовов;
· другие объекты.
4. Все виды измерений параметров трафика можно классифицировать следующим образом:
· по способу получения данных (автоматические и ручные);
· по способу регистрации данных (прямые и косвенные);
· по типу организации измерений (непрерывные, периодические и эпизодические);
· по охвату изучаемых объектов (сплошные и выборочные).
5. Примером непрерывного измерения нагрузки можно считать способ, основанный на контроле силы тока:
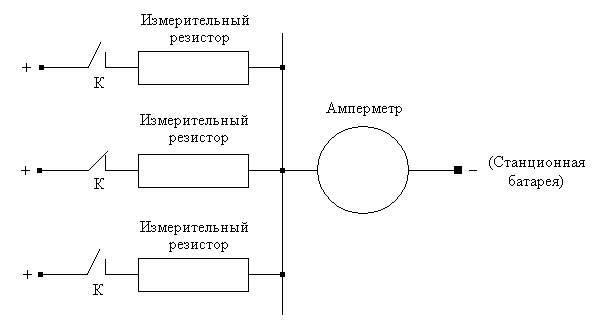
6. На практике сплошные измерения – до появления коммутационных станций с программным управлением – не производились из-за проблем финансового и организационного характера. В математической статистике всю изучаемую совокупность однородных элементов принято называть генеральной совокупностью. Часть генеральной совокупности, выбранной для измерений, называют выборочной совокупностью. Обычно исследуется поведение выборочной совокупности. Различают три способа измерения:
· непрерывное наблюдение;
· сканирование исследуемого процесса;
· анализ случайных событий.
Использование схемы с амперметром – один из примеров непрерывного наблюдения за изучаемой величиной.
7. В процессе измерений можно получить математическое ожидание для генеральной совокупности (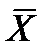 ) и для выборочной совокупности (
) и для выборочной совокупности (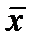 ). Пусть
). Пусть 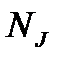 и
и 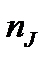 – численность
– численность 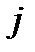 -ой группы элементов в генеральной и выборочной совокупности. Объем элементов определяется по таким формулам:
-ой группы элементов в генеральной и выборочной совокупности. Объем элементов определяется по таким формулам:
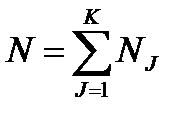 и
и 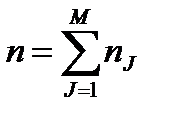 .
.
Степень расхождения между собой отдельных значений изучаемого процесса характеризуется дисперсией для и генеральной, и для выборочной совокупности:
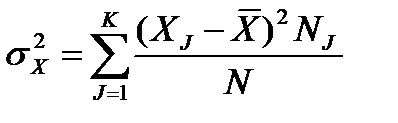 и
и 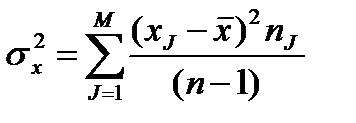 .
.
8. Пример рекомендаций по измерению трафика для полнодоступного пучка обслуживающих приборов. Будем считать, что время занятия равно единице, то есть 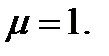 Если время измерений более чем в 20 раз превышает среднее время занятия, то для распределения статистических оценок можно использовать нормальный закон. Некоторые важные постулаты:
Если время измерений более чем в 20 раз превышает среднее время занятия, то для распределения статистических оценок можно использовать нормальный закон. Некоторые важные постулаты:
I Точность измерения растет пропорционально 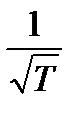 .
.
II Абсолютная среднеквадратическая погрешность измерений для обслуженной нагрузки (Y) при малой вероятности потерь (менее 0,01) определяется по такой формуле:
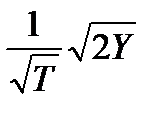 .
.
III Относительная среднеквадратическая погрешность измерений для обслуженной нагрузки (Y) определяется по такой формуле:
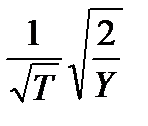 .
.
IV Абсолютная среднеквадратическая погрешность измерений при малой вероятности потерь (менее 0,01) определяется по такой формуле:
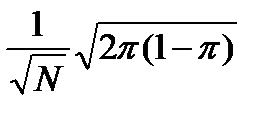 .
.
V Относительная среднеквадратическая погрешность измерений при малой вероятности потерь определяется по такой формуле:
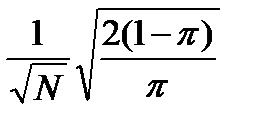 .
.
Допустим, что мы провели 10000 измерений вероятности потерь 0,01. Тогда относительная среднеквадратическая погрешность измерений составит примерно 14%, что не всегда удовлетворяет требованиям экспериментатора. В таблице приведено количество контрольных вызовов для выбранной точности оценки.
| Нормативное значение для показателя | Количество контрольных вызовов при точности: | ||
| 5% | 10% | 20% | |
| 0,01 | |||
| 0,02 | |||
| 0,03 | |||
| 0,04 | |||
| 0.05 |
9. Указания для проектирования сети содержатся в рекомендациях МСЭ (ITU) и национальных стандартах Администрации связи.
МСЭ рекомендует, чтобы при международной телефонной связи для 30 максимальных ЧНН потери не превышали 0,01. В то же время для 5 таких ЧНН разрешается устанавливать норму потерь в 0,07.
Примерные нормы для потерь вызовов "от абонента до абонента" (end-to-end) для ТФОП приведены в таблице
| Вид устанавливаемого соединения | Допустимые потери |
| В пределах ГТС | 0,03 – 0,05 |
| В пределах СТС | 0,12 |
| Внутризоновая связь | 0,07 |
| Междугородная связь (через ГТС) | 0,07 |
| Международная связь | 0,13 |
Примерные нормы для коэффициента эффективности вызовов в ТФОП приведены в таблице.
| Вид устанавливаемого соединения | Коэффициент эффективности вызовов |
| Местная связь (ГТС или СТС) | 0,5 – 0,6 (1,6 – 2,0 на разговор) |
| Внутризоновая связь | 0,4 – 0,5 (2,0 – 2,5 на разговор) |
| Междугородная связь (через ГТС) | 0,4 (2,5 на разговор) |
Средняя нагрузка по часам суток
Средняя пропускная способность одной линии пучка СЛ за сутки
Лекция 9 (2час) Звеньевые коммутационные системы.
Определение пропускной способности АТС
Рассмотрим простейшую модель АТС, состоящей всего из двух блоков (первый рисунок): коммутационное поле и устройство управления. На входе наблюдается случайный процесс 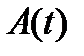 , а на выходе –
, а на выходе – 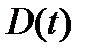 .
.
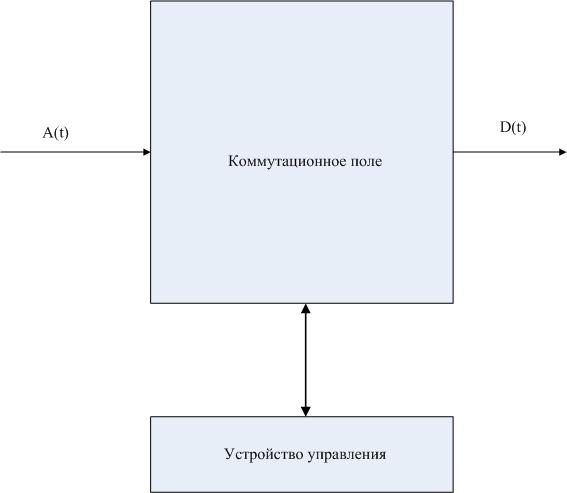
Простейшая модель АТС
Для такой АТС известны требования (рекомендации МСЭ серии Q.500):
· среднее значение длительности установления соединения через АТС не должно превышать 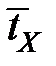 ;
;
· для 95% всех вызовов длительность установления соединения через АТС не должна превышать 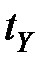 .
.
Традиционно задача расчета пропускной способности АТС состоит в том, что бы для поступающего трафика определить минимум пропускной способности коммутационного поля и устройства управления.
Допустим, что процесс 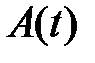 – простейший поток с интенсивностью
– простейший поток с интенсивностью 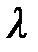 . Будем также считать, что обслуживание любого вызова есть случайная величина с функцией распределения
. Будем также считать, что обслуживание любого вызова есть случайная величина с функцией распределения 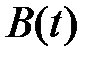 с коэффициентом вариации
с коэффициентом вариации 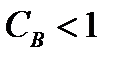 .
.
Очевидно, что можно выбрать две модели: 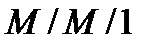 и
и 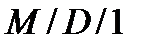 , для которых полученные оценки будут определять верхнюю и нижнюю границы большинства вероятностно-временных характеристик (ВВХ).
, для которых полученные оценки будут определять верхнюю и нижнюю границы большинства вероятностно-временных характеристик (ВВХ).
По формулам, определяющим математическое ожидание длительности задержки заявок и функцию распределения, можно найти две величины для интенсивности обслуживания: 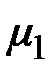 и
и 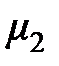 . Очевидно, что
. Очевидно, что 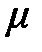 (истинное значение интенсивности обслуживания) должно отвечать такому условию:
(истинное значение интенсивности обслуживания) должно отвечать такому условию:
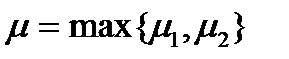 . (1)
. (1)
Для системы 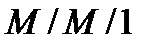 величины
величины 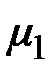 и
и 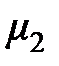 определяются из известных соотношений:
определяются из известных соотношений:
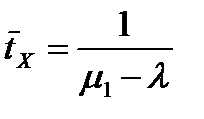 .
. 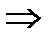
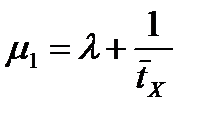 ,
,  (2)
(2)
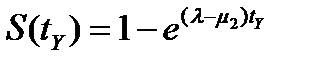 .
. 
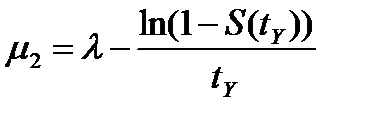 .
.
Для системы 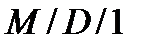 величина
величина 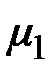 определяется следующим образом:
определяется следующим образом:
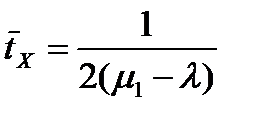 .
. 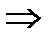
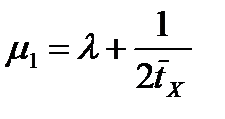 . (3)
. (3)
Допустим, что в результате расчетов были выбраны верхняя и нижняя границы для интенсивности обслуживания: 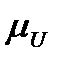 и
и 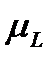 . Если различие между ними существенно (с учетом рассматриваемой задачи), то необходимо перейти к анализу СМО вида
. Если различие между ними существенно (с учетом рассматриваемой задачи), то необходимо перейти к анализу СМО вида 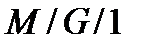 . Если же различие не представляется существенным, то величина
. Если же различие не представляется существенным, то величина 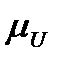 сопоставляется с неким рядом
сопоставляется с неким рядом 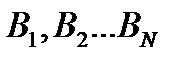 , который определяет возможные реализации аппаратно-программных средств АТС.
, который определяет возможные реализации аппаратно-программных средств АТС.
Если оценке 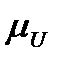 соответствует величина
соответствует величина 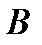 , которая лежит в пределах
, которая лежит в пределах 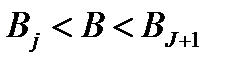 , то пропускная способность выбирается как
, то пропускная способность выбирается как 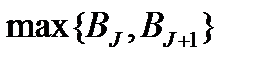 .
.
Следует различать вероятностно-временные характеристики, которые важны для коммутационного поля и устройства управления.
В рассматриваемом примере речь идет об устройстве управления. Для оценки пропускной способности коммутационного поля можно использовать первую формулу Эрланга.
Одна и та же величина интенсивности нагрузки пожжет быть получена за счет различных сочетаний сомножителей в формул
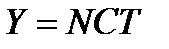 . (4)
. (4)
При большом значении числа обрабатываемых вызовов (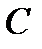 ) и малом времени обслуживания (характерный пример – справочная служба) следует тщательно рассчитывать ВВХ, связанные с устройством управления. При большом значении времени обслуживания и малом числе вызовов (например, для модемного пула) наибольший интерес вызывает расчет ВВХ для поля коммутации и транспортных ресурсов.
) и малом времени обслуживания (характерный пример – справочная служба) следует тщательно рассчитывать ВВХ, связанные с устройством управления. При большом значении времени обслуживания и малом числе вызовов (например, для модемного пула) наибольший интерес вызывает расчет ВВХ для поля коммутации и транспортных ресурсов.
2. Задачи, связанные с услугой "Прямая линия"
Услугу "Прямая линия" (второй рисунок) можно представить как симбиоз двух услуг Интеллектуальной сети (ИС): вызов, оплачиваемый вызываемым абонентом (FreePhone), и массовый опрос (MassCalling). Один из первых примеров практической реализации услуги "Прямая линия" – организация "Прямой линии Президента Российской Федерации".
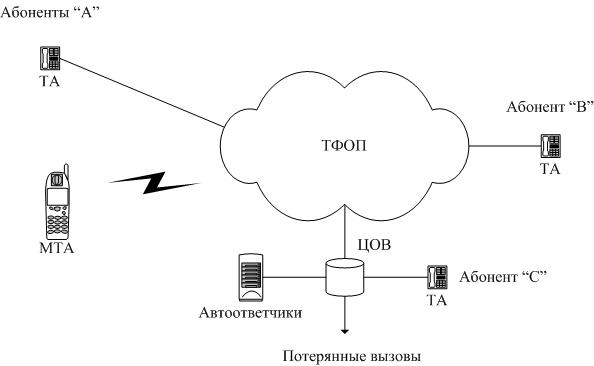
Модель услуги "Прямая линия"
Рекомендуемые требования к обслуживанию трафика для услуги "Прямая линия" перечислены в таблице 1. Они определены для ЦОВ (центр обслуживания вызовов) в час наибольшей нагрузки (ЧНН).
Таблица 1
| Требование к услуге "Прямая линия" по обслуживанию трафика | Рекомендуемая величина |
| Вероятность потери вызова в ЧНН | 5% |
| Вероятность ожидания ответа в ЦОВ | 50% |
| Среднее время ожидания ответа в ЦОВ | 30 с |
| Время ожидания ответа в ЦОВ для 95% вызовов | 60 с |
На двух следующих графиках показаны тенденции изменения нагрузки (по часам суток) и длительности занятия.
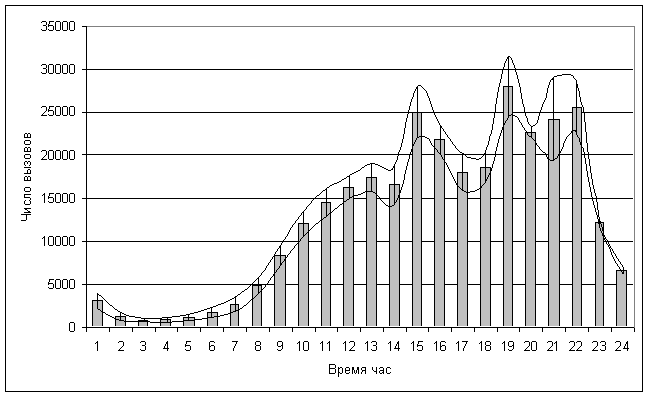
Изменение нагрузки за сутки
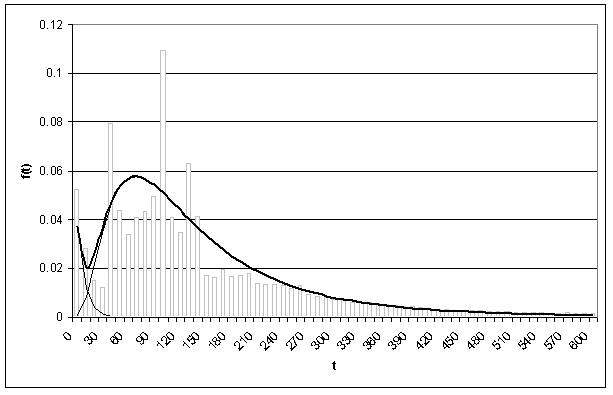
Изменение времени занятия
Для подобных моделей расчет всех ВВХ осуществляется имитационным моделированием.
 2015-03-27
2015-03-27 1541
1541








