Уравнение состояния провода. Исходный режим

Механическое напряжение в проводе изменяется в зависимости от удельной нагрузки на провод и температуры окружающего воздуха. Для двух любых режимов i и j, характеризующихся удельными нагрузками р _i и р _j и температурами Q_i и Q_j, механические напряжения в проводе _i и _j в этих режимах связаны уравнением состояния провода, которое имеет следующий вид:

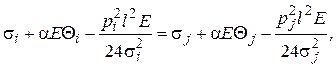(5.14)

где a - температурный коэффициент линейного удлинения материала провода, 1/^оС;

Е – модуль упругости материала провода, даН/мм²;

l – расчетная длина пролета, м.

При дальнейшем изложении порядка расчета провода на прочность полагается, что опора выбрана и, следовательно, известны ее характеристики и геометрические размеры (см. приложение 3). В частности, известен габаритный пролет l _г. Это пролет такой длины, в котором в режиме с максимальной стрелой провеса при установке опор на идеально ровной местности точно выполняется установленный ПУЭ габарит ВЛ (расстояние от низшей точки провисания провода до земли).

Расчетная длина пролета выбирается по габаритному пролету l =(0,8...0,9) l _г. Меньшие значения расчетного пролета принимаются для населенной местности, большие – для ненаселенной.

По уравнению состояния (5.14) необходимо определить механические напряжения в проводе в режимах низшей температуры (р ₁, Q_min), среднегодовой температуры (р ₁, Q_ср) и наибольшей внешней нагрузки (р _max, Q_г = Q_в = -5^oC) и проверить условия (5.1).

Прямое решение уравнения (5.14) для двух любых режимов невозможно, поскольку это уравнение содержит два неизвестных напряжения: _i и _j.

Введем понятие исходного режима. Это такой режим, в котором механическое напряжение в проводе равно допустимому значению, при этом во всех других режимах механическое напряжение в проводе меньше допустимого.

Поскольку для расчета механической прочности провода необходимо рассмотреть только три режима, а исходным режимом может быть любой из этих трех режимов, воспользуемся методом перебора возможных вариантов. Таких вариантов три.

1. Исходный режим - режим наибольшей внешней нагрузки с параметрами р _max и Q_г = Q_в = -5^оС. Напряжение в проводе в этом исходном режиме считается известным и равным допустимому для этого режима, т. е. _рmax = [_pmax]. Подставив параметры исходного режима в левую часть уравнения состояния провода (5.14), вычислим ее значение:

С = [_pmax] + E Q_г - р _max² l ² E / 24[_pmax]². (5.15)

В правую часть уравнения (5.14) подставим параметры режима низшей температуры р ₁ и Q_min. Уравнение (5.14) сведется к неполному кубическому уравнению вида

_Qmin³+ A _Qmin² + B = 0, (5.16)

где A = E Q_min – C;

B = – р ₁² l ² E / 24.

Решив уравнение (5.16), найдем напряжение в проводе в режиме низшей температуры _Qmin.

Далее в правую часть уравнения состояния (5.14) подставим параметры режима среднегодовой температуры р ₁ и Q_ср. Уравнение (5.14) сведется к неполному кубическому уравнению

_Qср³+ A _Qср² + B = 0, (5.17)

где A = E Q_ср - C;

B = - р ₁² l ² E / 24.

Решив уравнение (5.17), найдем напряжение в проводе в режиме среднегодовой температуры _Qср.

Проверим условия (5.1). Если они выполняются, исходный режим выбран верно. В противном случае рассматриваем вариант 2.

2. Исходный режим - режим низшей температуры с параметрами р ₁ и Q_min. Напряжение в проводе в этом исходном режиме считается известным и равным допустимому для этого режима, т. е. _Qmin = [_Qmin]. Подставив параметры этого режима в левую часть уравнения состояния провода (5.14), вычислим ее значение:

С = [_Qmin] + E Q_min - р ₁² l ² E / 24[_Qmin] ². (5.18)

В правую часть уравнения состояния (5.14) подставим параметры режима наибольшей внешней нагрузки р _max и Q_г = -5^оС. Уравнение (5.14) сведется к неполному кубическому уравнению

_рmax³ + A _pmax² + B = 0, (5.19)

где A = E Q_г – C;

B = - р _max² l ² E / 24.

Решив уравнение (5.19), найдем напряжение в проводе в режиме наибольшей внешней нагрузки _рmax.

Далее в правую часть уравнения состояния (5.14) подставим параметры режима среднегодовой температуры р ₁ и Q_ср. Уравнение (5.14) сведется к неполному кубическому уравнению

_Qср³ + A _Qср² + B = 0, (5.20)

где A = E Q_ср – C;

B = - р ₁² l ² E / 24.

Решив уравнение (5.16), найдем напряжение в проводе в режиме среднегодовой температуры _Qср.

Проверим условия (5.1). Если они выполняются, исходный режим выбран верно. В противном случае рассматриваем вариант 3.

3. Исходный режим - режим среднегодовой температуры с параметрами р ₁ и Q_ср. Напряжение в проводе в этом исходном режиме считается известным и равным допустимому для этого режима, т. е. _Qср = [_Qcp]. Подставив параметры этого режима в левую часть уравнения состояния провода (5.14), вычислим ее значение:

С = [_Qcp] + E t _cp- р ₁² l ² E / 24[_tcp] ². (5.21)

В правую часть уравнения состояния (5.14) подставим параметры режима низшей температуры р ₁ и Q_min. Уравнение (5.14) сведется к неполному кубическому уравнению

_Qmin³ + A _Qmin² + B = 0, (5.22)

где A = E Q_min – C;

B = - р ₁² l ² E / 24.

Решив уравнение (5.18), найдем напряжение в проводе в режиме низшей температуры _Qmin.

Далее в правую часть уравнения состояния (5.14) подставим параметры режима наибольшей внешней нагрузки р _max и Q_г = -5^оС. Уравнение (5.14) сведется к неполному кубическому уравнению

_рmax³ + A _рmax² + B = 0, (5.23)

где A = E Q_г – C;

B = – р _max² l ² E / 24.

Решив уравнение (5.23), найдем напряжение в проводе в режиме наибольшей внешней нагрузки _рmax.

Проверим условия (5.1). Если они выполняются, исходный режим выбран верно.

Следует отметить, что для климатических условий нашей страны в подавляющем большинстве случаев исходным оказывается режим наибольшей внешней нагрузки.