2015-03-20
5784
Рассмотрим пример направленного графа электрической сети, изображенного на рис. 3.10.
Для удобства записи в матричной форме параметров ветвей присвоим каждой ветви ее порядковый номер (на рис. 3.10 курсив). Составим матрицу соединений M для этого графа:
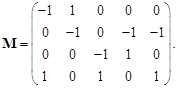(3.10)
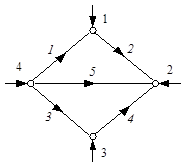
Рис. 3.10. Пример графа
электрической сети
Умножим эту матрицу на матрицу токов ветвей, будем иметь:
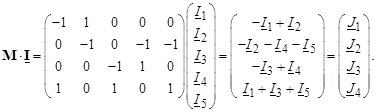(3.11)
Полученное соотношение является первым законом Кирхгофа в матричной форме записи
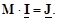(3.12)
Так как к узлам графа электрической сети еще присоединены другие поперечные ветви с ЭДС и проводимостью шунта, то задающий ток в (3.12) включает в себя также токи данных ветвей
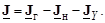(3.13)
Здесь: J г – матрица токов генерации (ветви с ЭДС), которые определяются через мощности генерации;
J н – матрица токов нагрузки, которые определяются через мощности нагрузки (имеет обратное направление – от узла);
J Y – матрица токов в проводимостях шунтов, которые зависят от проводимости шунта из матрицы Y N и напряжения в узле из матрицы U (также имеет обратное направление – от узла, так как моделирует потребление мощности).
Умножим транспонированную матрицу соединений М T на матрицу узловых напряжений, получим:
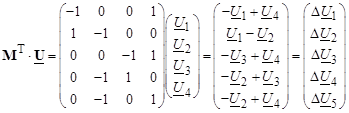(3.14)
или
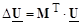. (3.15)
По закону Ома в матричной форме записи имеем
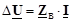(3.16)
или
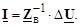(3.17)
Подставим в (3.12) выражение для матрицы токов ветвей (3.17) и затем (3.15), получим
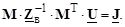(3.18)
Введем обозначение
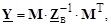(3.19)
тогда (3.18) приобретет вид
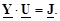(3.20)
Полученное соотношение является уравнением узловых напряжений (потенциалов) в матричной форме записи. Матрицу Y называют матрицей узловых проводимостей электрической сети. Рассмотрим структуру этой матрицы, для чего выполним матричные перемножения в (3.19). Заметим, что обратная матрица сопротивлений ветвей легко получается в силу своего диагонального вида – ее элементы суть обратные величины к сопротивлениям ветвей и являются проводимостями продольных ветвей.
Вначале перемножим первые две матрицы матричного произведения (3.19):
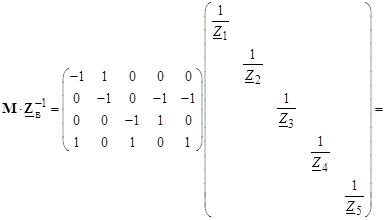
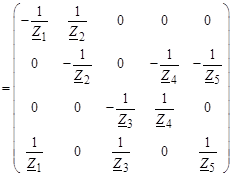. (3.21)
Полученную матрицу умножим справа на матрицу M T. В результате получим:
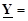
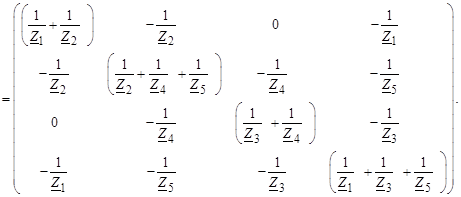
(3.22)
Из полученной матрицы можно сделать следующие выводы о вычислении ее элементов.
1. Элементы, расположенные на главной диагонали матрицы, вычисляются как сумма проводимостей ветвей, подходящих к соответствующему узлу:
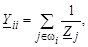(3.23)
где Y ii – диагональный элемент матрицы Y;
Z j – сопротивление j -й ветви;
w i – множество номеров узлов, связанных с i -м узлом.
2. Недиагональные элементы равны проводимостям ветвей, имя каждой из которых состоит из номеров узлов, соответствующих номеру строки и номеру столбца, на пересечении которых находится данный элемент, и взятых с противоположным знаком. Матрица Y является симметричной матрицей.
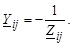(3.24)
Запишем уравнение узловых напряжений для узла с номером i:
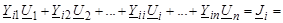
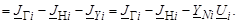(3.25)
Объединив подобные члены, получим, что в диагональные элементы матрицы Y войдут дополнительные слагаемые Y Ni:
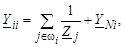(3.26)
т. е. диагональный элемент будет равен сумме проводимостей всех подходящих к i -му узлу ветвей, включая поперечную ветвь – шунт Y Ni.
Задающие токи узлов в (3.20) будут состоять только из токов генерации и токов нагрузки.
В случае отсутствия связей с нейтральной плоскостью N система уравнений (3.20) не имеет единственного решения, так как в этом случае определитель матрицы Y равен нулю. Сумма всех задающих токов в такой сети равна нулю:
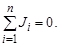(3.27)
Следовательно, среди всех n узлов можно выделить узел, например с номером n, ток в котором равен
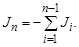(3.28)
Для уравнений узловых напряжений это означает, что одно уравнение лишнее, т. е. зависит от остальных уравнений и может быть получено через сумму всех остальных уравнений. Так как ток в этом узле может быть получен из баланса токов в сети (3.28), то его называют балансирующим. Обычно это шины мощной электростанции или системы.
Таким образом, из системы (2.20) исключается одно уравнение и тогда получается система независимых линейных уравнений порядка
n – 1. Однако, поскольку число неизвестных напряжений по-прежнему равно n, в одном из узлов следует задать напряжение по величине и фазе так, чтобы все напряжения вычислялись относительно этого известного напряжения. Такой узел в сети называется базисным. Обычно фазу напряжения базисного узла принимают равной нулю, т. е. вектор напряжения базисного узла совмещают с действительной осью. Остальные узлы называют независимыми узлами.
Во многих случаях балансирующий узел и базисный узел совмещают, и в дальнейшем будем считать, что это один и тот же узел.
Таким образом, с исключением уравнения для базисного балансирующего узла с номером n будем иметь систему уравнений (3.20) с числом уравнений n – 1, однако в эти уравнения будет входить слагаемое с заданным напряжением базисного узла.
Изменим номер базисного балансирующего узла. Пусть его номер есть 0 (ноль). Тогда уравнение (3.20) приобретет следующий вид:
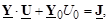(3.29)
где Y 0 – матрица проводимостей ветвей, связывающих независимые узлы с базисным балансирующим узлом;
U 0 – напряжение базисного узла (скаляр).
Матрица узловых проводимостей в (3.29) имеет порядок n – 1 и определется через матрицу инциденций M, в которой нет одной строки, соответствующей балансирующему узлу.
Необходимо заметить, что во всех уравнениях, где одновременно присутствуют токи и напряжения (3.16), (3.17), (3.18), (3.20), (3.25) и (3.29), напряжения даны в фазных значениях, хотя индекс (буква «ф») для простоты не записывался. Эти же уравнения можно считать записанными и для линейных напряжений, однако токи будут увеличенными в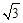 
раз, и для вычисления истинных токов их следует уменьшать в .
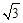3.5. Формы линейных уравнений
установившегося режима и их решение
Известными независимыми переменными в уравнениях установившегося режима могут быть задающие токи узлов и напряжение базисного узла. В этом случае решение уравнения (3.29) может быть записано в виде
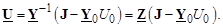(3.30)
Здесь Z – матрица узловых сопротивлений.
Численное решение системы уравнений (3.29) выполняется методом Гаусса или другим методом решения системы линейных алгебраических уравнений.
В случае, когда известны мощности в узлах сети – задающие мощности S i, токи можно вычислить приближенно через номинальные напряжения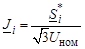 
(i = 1,…, n – 1). Задающие мощности так же, как и токи, складываются из мощности генерации и мощности нагрузки:
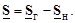(3.31)
Другой приближенный подход связан с представлением задающих токов через напряжения и проводимости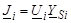 
, где Y Si – проводимость генерации и/или нагрузки (схема замещения). Для i -го узла имеем:
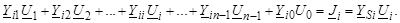(3.32)
Объединив подобные члены, получим
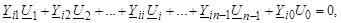(3.33)
где в элемент Y ii входит проводимость Y Si. Знак перед этой проводимостью зависит от того, какая мощность преобладает в узле: плюс, если нагрузка, и минус, если генерация. В матричной форме записи:
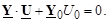(3.34)
Решение матричного уравнения (3.34) запишется в виде
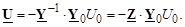(3.35)
Комплексную матрицу узловых проводимостей Y иногда представляют в блочной форме через ее вещественную G и мнимую B составляющие, и тогда система уравнений (3.34) становится системой с вещественными величинами:
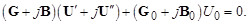(3.36)
После перемножения двучленов в (3.35) будем иметь:
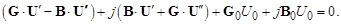(3.37)
Приравняем отдельно вещественные и мнимые части полученного уравнения и получим два матричных уравнения с вещественными величинами:
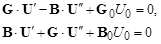(3.38)
или в компактной форме записи:
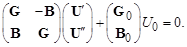(3.39)
Решение (3.39) запишется в виде
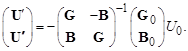(3.40)
Пример 2. Рассчитаем напряжения в узлах и токи в ветвях схемы электрической сети, граф которой изображен на рис. 3.10. Исходные данные для расчета и расчет представлены в системе Mathcad.
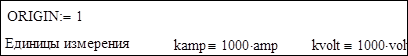
Исходные данные
Напряжение базисного узла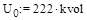 
Сопротивления ветвей и задающие токи узлов:
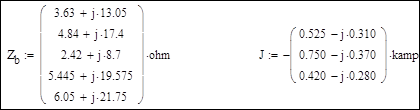
Расчетные данные
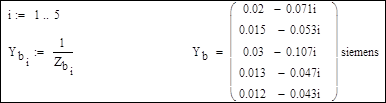
Модель электрической сети
1. Составление матрицы инциденций узлов и ветвей M:
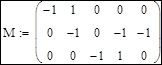
2. Формирование диагональной матрицы проводимостей ветвей Y:
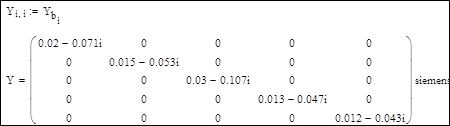
3. Составление матрицы-столбца проводимостей ветвей, связывающих узлы схемы с базисным узлом Y 0:
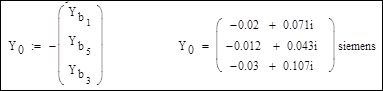
4. Получение матрицы узловых проводимостей Y:
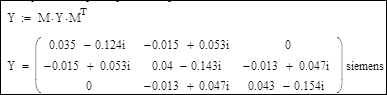
Вычисления
1. Решение системы линейных уравнений методом обратной матрицы:
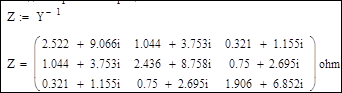
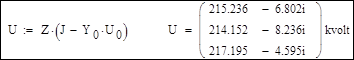
2. Расчет других параметров режим сети:
|
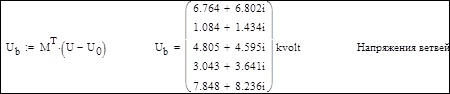
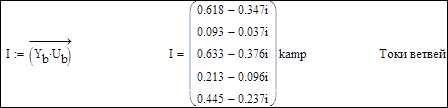
3. Проверка результатов: сумма задающих токов должна быть равна току балансирующего узла с обратным знаком:
|
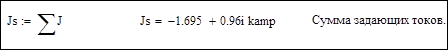
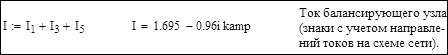
3.6. Нелинейные уравнения
установившегося режима
Так как во многих случаях расчеты ведутся при заданных мощностях нагрузок и генерации, то их следует ввести в уравнения установившегося режима.
Мощность в трехфазной сети в симметричных режимах выражается суммарной мощностью всех трех фаз:
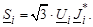(3.41)
В матричной форме это выражение можно записать, используя операцию диагонализации матрицы U. Матрица diag{ U } есть квадратная матрица, в которой элементы матрицы U расположены по главной диагонали, а все остальные элементы равны нулю. Тогда
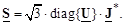(3.42)
Уравнение установившегося режима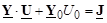 
записано для фазных токов и напряжений. Умножим обе части этого уравнения на 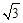и применим к величинам этого уравнения операцию сопряжения, получим
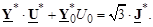(3.43)
В левой части этого уравнения после умножения на 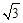напряжения стали линейными.
Умножим левую и правую части уравнения (3.43) слева на матрицу diag{ U }, получим
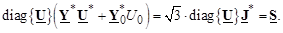(3.44)
Система уравнений (3.44) является системой нелинейных уравнений установившегося режима. В зависимости от формы представления комплексных величин применяют две основные формы этой системы уравнений.
Вначале рассмотрим алгебраическую форму записи. Для i -го узла имеем:
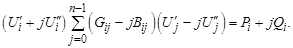(3.45)
После перемножения двучленов и разделения уравнения на два уравнения с вещественными величинами получим систему 2(n – 1) алгебраических уравнений
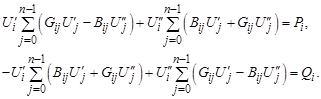(3.46)
Здесь i = 1,…, n – 1.
Тригонометрическая форма нелинейных уравнений установившегося режима может быть получена, если комплексные величины в уравнении (3.44) записать в виде
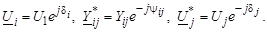(3.47)
Тогда
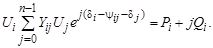(3.48)
Уравнение (3.48) в тригонометрической форме запишется как
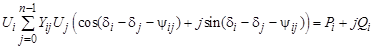, (3.49)
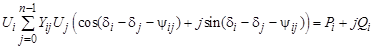, (3.50)
и после разделения на два вещественных уравнения
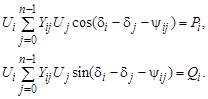(3.51)
Обычно вместо угла y ij используют дополняющий до 90° угол a ij. a ij = 90 - y ij, y ij = 90 - a ij.
Тогда cos(d i – d j – y ij) = cos(d i – d j – 90° + a ij), а с учетом четности функции косинус cos(d i – d j – 90°+ a ij) = cos(90° – d i + d j – a ij). Имея
в виду, что cos(90° – b) = sin(b), получим cos(90° – d i + d j – a ij) =
= sin(d i – d j + a ij).
Аналогично sin(d i – d j – y ij) = sin(d i – d j – 90 + a ij) = –sin(90° – d i +
+ d j – a ij), в силу нечетности функции синус. Так как sin(90° – b) =
= cos(b), получим –sin(90° – d i + d j – a ij) = –cos(d i – d j + a ij). Подставляя полученные соотношения в (3.51), будем иметь:
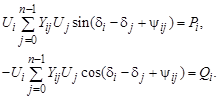(3.52)
В полученной системе нелинейных уравнений установившегося режима искомыми переменными являются модули и фазовые углы напряжений, в то время как в уравнениях (3.46) неизвестными являются вещественная и мнимая составляющие напряжений.
Пример 3. Рассчитаем напряжения в узлах и потоки мощности в ветвях схемы сети, граф которой изображен на рис. 3.10. Исходные данные для расчета и расчет представлены в системе Mathcad.
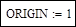
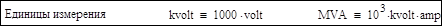
Исходные данные
Погонные параметры ЛЭП:
|
|
|
|
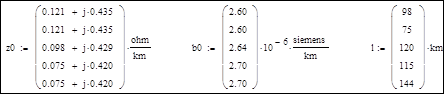
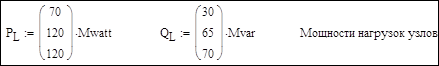
Модель электрической сети
1. Расчетные параметры ЛЭП:
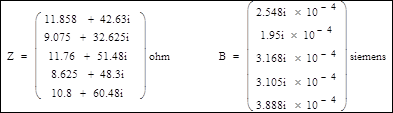
2. Составление матрицы инциденций узлов и ветвей M:
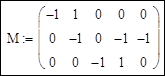
3. Формирование матрицы проводимостей ветвей Yb:
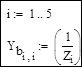
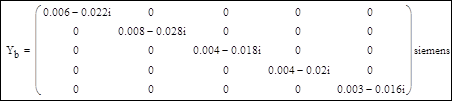
4. Получение матрицы узловых проводимостей Y:
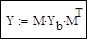
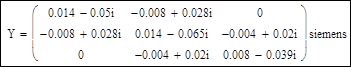
5. Емкостные проводимости поперечных ветвей Yc:
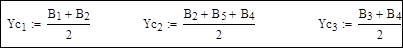
6. Корректировка диагональных элементов матрицы Y
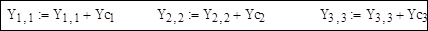
7. Расширение матрицы узловых проводимостей добавлением столбца для базисного балансирующего узла:
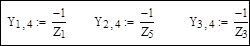
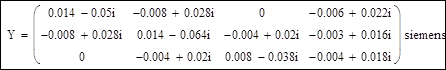
Вычисления
1. Решение системы нелинейных уравнений установившегося режима
Начальные приближения:
Решающий блок – приближенное решение:
|
|
|
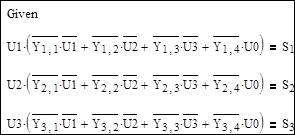
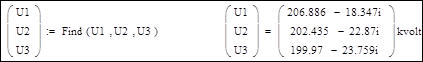
Результат решения – узловые напряжения (в экспоненциальной форме записи):
2. Расчет других параметров режима сети
Напряжения в начале и конце ветвей и токи узлов ветвей:
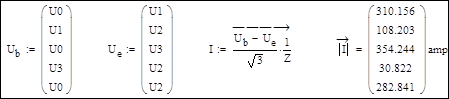
Мощности в начале и конце ветвей:
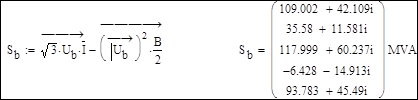
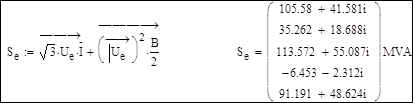
Потери мощности в ветвях:
3. Проверка результатов расчета: сумма мощностей узлов, потерь и зарядной мощности в сети должна быть равна мощности балансирующего узла:
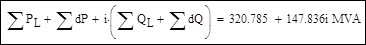
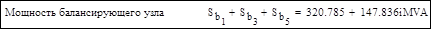
3.7. Моделирование генераторных узлов
электрической сети
Генераторными узлами называют узлы, в которых генерируется активная мощность. Реактивная мощность, как правило, также генерируется в узлах. Генераторные узлы – это шины электрических станций или шины мощной системы, схема которой не входит в модель для расчетной схемы. Моделируются генераторные узлы по-разному:
· так же, как и узел нагрузки, – постоянными значениями активной и реактивной мощности, но с противоположным знаком;
· постоянным значением активной мощности и фиксированным значением модуля напряжения в узле. Реактивная мощность не известна и подлежит расчету;
· генераторный узел – это базисный и балансирующий узел одновременно. Активная и реактивная мощности узла подлежат вычислению;
· генераторный узел – это базисный узел, но с известными значениями активной и реактивной мощности – заданы все четыре независимых параметра режима – P, Q, U, d;
· генераторный узел – это балансирующий узел, но напряжение в нем не известно ни по модулю, ни по фазе. Подлежат определению все четыре независимых параметра режима – P, Q, U, d.
При фиксации активной мощности и модуля напряжения обычно в уравнения установившегося режима входит уравнение для активной мощности узла (3.46) и уравнение вида: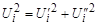 
, где Ui задано, а 
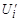и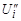 
подлежат определению.
В тех случаях, когда для одного из узлов требуется задать все четыре независимых параметра режима – P, Q, U, d (базисный узел), то в сети должен появиться узел, в котором не известен ни один из этих четырех параметров – балансирующий узел. Происходит разделение балансирующего и базисного узлов.
Форма уравнений установившегося режима меняется, а именно –перестраивается матрица узловых проводимостей. Так, например, если для графа сети на рис. 3.10 базисным стал узел 2, а балансирующим остался узел 0, то матрица Y принимает вид:
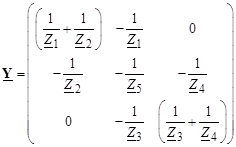
Пример 4. Рассчитаем напряжения в узлах электрической сети (рис. 3.11) при несовпадении базисного и балансирующего узлов.
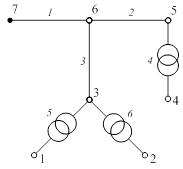
Рис. 3.11. Схема сети примера 4
Ветви 1, 2 и 3 графа – это линии электропередачи 110 кВ, выполненные проводом марки АС-120/19 с погонными параметрами r 0 = 0,249 Ом/км;
x 0 = 0,427 Ом/км; b 0 = 2,6 мкСм/км. Три двухобмоточных трансформатора имеют номинальные напряжение обмоток высшего и низшего напряжения соответственно 115 и 11 кВ.
Параметры линий и трансформаторов приведены в табл. 3.1 и 3.2
Таблица 3.1
Параметры ЛЭП
| Наименование | Начало | Конец | Длина, км | R, Ом | X, Ом | B, мкСм |
| Л-1 | 7,2 | 1,79 | 3,07 | 19,2 | ||
| Л-2 | 3,4 | 0,85 | 1,45 | 9,0 | ||
| Л-3 | 12,3 | 3,06 | 5,25 | 32,7 |
Таблица 3.2
| Наименование | Начало | Конец | Тип | R, Ом | X, Ом | D P, кВт | D Q, квар |
| Т-1 | ТМН-6300/110 | 15,99 | 220,42 | ||||
| Т-2 | ТДН-10000.110 | 7,93 | 136,86 | 15,1 | |||
| Т-3 | ТДН-16000/110 | 4,44 | 86,79 | 21,3 |
Мощности нагрузки даны для шин низкого напряжения трансформаторов – узлы 1 (T1), 2 (T2) и 4 (Т3).
P T1 + jQ T1 = 5,0 + j 2,5 МВ·А; P T2 + jQ T2 = 7,0 + j 3,5 МВ·А;
P T1 + jQ T1 = 12,0 + j 6,0 МВ·А.
Приведем два расчета: вначале расчет, когда базисный и балансирующий узлы совпадают – узел 7; затем – балансирующим остается узел 7, а базисным является узел 5. Расчеты выполним в системе Mathcad. Сопротивления в омах, проводимости в сименсах, напряжения в киловольтах, мощности в мегаваттах.
Системная переменная начального номера массивов:
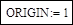
Исходные данные по линиям:
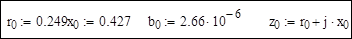
Расчетные данные по линиям:
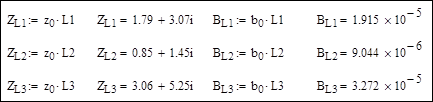
Исходные и расчетные данные по трансформаторам:
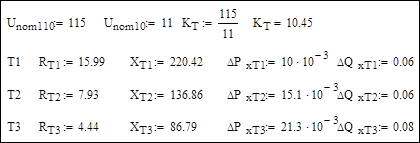
Исходные данные по мощностям нагрузок:
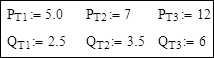
Вектор проводимостей продольных ветвей и вектор проводимостей связи независимых узлов с базисным узлом (в первом расчете – узел 7):
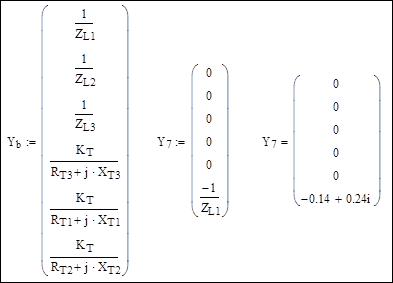
Матрица инциденций M и матрица узловых проводимостей:
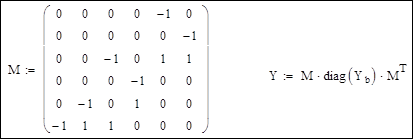
Корректировка диагональных элементов матрицы узловых проводимостей для учета поперечных ветвей П-образных схем замещения линий и трансформаторов:
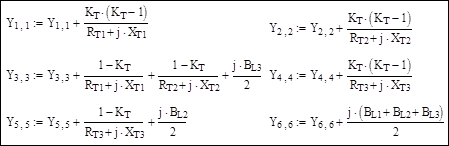
Результирующая матрица узловых проводимостей:
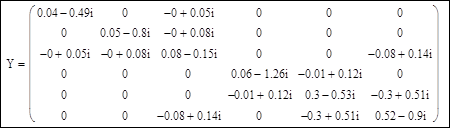
Матрица задающих мощностей в узлах сети:
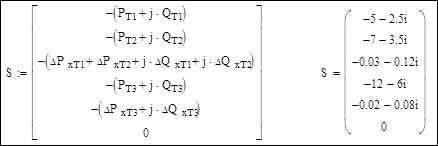
Напряжение в базисном узле и начальные приближения напряжений в узлах:
Решающий блок:
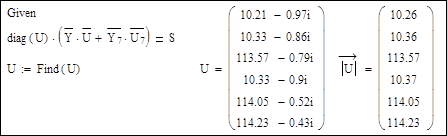
Выполним расчет для случая, когда базисным узлом является узел 5, а балансирующим остается узел 7. Поменяем в матрице Y столбец, соответствующий узлу 5; теперь это столбец проводимостей связи узлов с узлом 7. Прежний столбец матрицы Y для узла 5 войдет в систему уравнений умноженным на известное напряжение узла 5 – напряжение базисного узла.
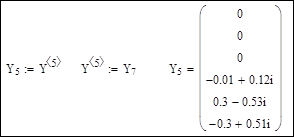
Матрица узловых проводимостей для нового расчета:
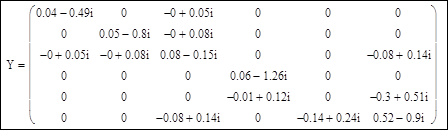
Матрица не является симметричной, и на диагонали имеется один нулевой элемент.
Напряжение нового базисного узла возьмем для сравнения результатов расчета таким, каким оно получилось в предыдущем расчете:
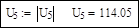
Решающий блок:
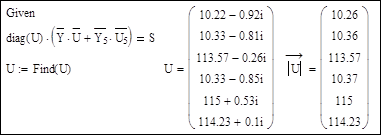
В векторе узловых напряжений на 5-м месте расположено значение напряжения в узле 7, которое являлось искомым и получилось именно таким, каким было задано в первом расчете. Все остальные напряжения совпадают с прежними значениями.
