Сочетания

1) Сочетания без повторений.

В некоторых задачах по комбинаторике не имеет значения порядок расположения объектов в той или иной совокупности. Важно лишь то, какие именно элементы ее составляют. В таких ситуациях мы имеем дело с сочетаниями.

Определение 3: Сочетания из 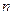элементов по 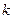элементов (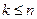) – это расстановки, отличающиеся друг от друга составом, но не порядком элементов. Обозначают: .

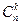В данном случае в расстановках важен состав, а не порядок элементов в подмножестве. Если две расстановки отличаются только порядком следования элементов, то с точки зрения сочетаний они не различимы. Элементы в этих расстановках не повторяются.

Теорема 4: Число сочетаний находится по следующей формуле:

.

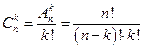Доказательство: Если из произвольного 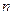-элементного множества выбраны 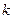элементов, то их можно пронумеровать номерами 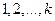числом способов, равным 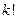. Оставшиеся 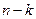элементов можно занумеровать номерами 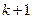, , 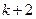…, 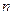всего 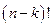способами. Кроме того, сам отбор 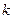элементов из 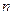элементов можно осуществить 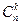способами. Таким образом, мы получили 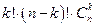вариантов нумерации полного множества из 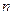элементов, которых всего 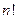. Поэтому имеем 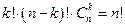, откуда имеем:

.

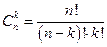Теорема доказана.

Отсюда видно, что число размещений 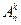в 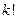раз больше числа соответствующих сочетаний 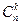. Другими словами, чтобы посчитать все сочетания 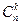, нужно исключить из всех размещений 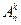подмножества, отличающиеся порядком (их будет 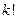штук), т.е. 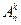делят на .

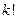Следствие: Выведенная формула совпадает с формулой для числа повторений из 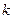элементов одного типа и 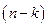элементов второго типа:

.

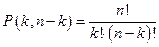Иными словами справедливо равенство: .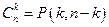

Примеры: Выбор делегации, число призеров в соревновании и т. д.

Замечание: , .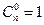

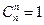Существенное отличие числа сочетаний от числа соответствующих размещений состоит в том, что для размещений важен состав и порядок элементов в подмножествах, а для сочетаний важен только состав.

2) Сочетания с повторениями.

Пусть имеется предметы 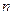различных типов. Сколько 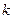комбинаций можно сделать из них, если не принимать во внимание порядок элементов? Эту задачу в общем виде можно решать точно так же, как задачу с пирожными.

Задача: В кондитерском магазине продаются пирожные 4 сортов: наполеон, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Зашифруем каждую покупку с помощью нулей и единиц. Напишем столько единиц, сколько куплено наполеонов, затем пишем 0, чтобы отделить пирожные одного типа от другого и т.д. Тогда каждой покупке будет соответствовать последовательность из семи единиц и трех нулей в различном порядке. Число всех таких покупок тогда будет равно:

.

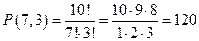Для числа сочетаний с повторениями существует формула:

.

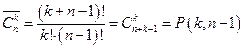Доказательство. Пронумеруем элементы исходного множества числами от 1 до 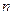. Пусть в одно из сочетаний с повторениями вошло 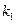элементов под номером 1, 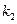элементов под номером 2, …, 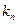элементов под номером 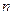. Поскольку составляются группы из 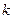объектов, то .

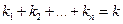Изобразим это сочетание с повторениями в виде последовательности из нулей и единиц. Единица будет обозначать каждый отдельный объект сочетания, нуль – разделитель между группами.

Поскольку сумма всех 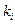равна 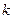, то в построенной последовательности содержится 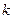единиц, а так как имеется 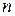различных по составу групп, то разделителей (нулей) будет 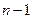. Верно обратное: каждой такой последовательности соответствует сочетание с определенными повторениями.

Таким образом, задача свелась к поиску ответа на вопрос: сколько различных последовательностей длины 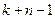можно составить из 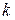единиц и 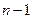нулей? Это есть число перестановок с повторениями из 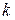единиц и 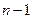нулей:

.

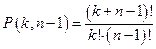А так как 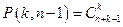, то формула доказана.