Основные комбинаторные формулы

Начнем с основных принципов комбинаторики, т.е. с правил.

Существует два общих правила комбинаторики: правило сложения и правило умножения.

Правило умножения:

Пусть составляются всевозможные строки 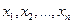длины 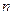. Пусть первая компонента строки может быть выбрана числом способов, равным 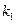. После того, как первая компонента выбрана и независимо от того, как она выбрана, вторая компонента выбирается числом способов, равным 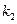. Далее аналогично. Последняя компонента выбирается числом способов, равным 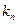. Тогда количество всех построенных строк равно произведению: .

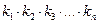Правило сложения:

Если некоторый элемент 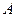можно выбрать 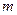различными способами, а другой элемент 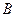выбирается 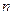способами, то объект «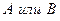» можно выбрать 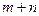способами.

Доказательство. Пересчитаем элементы объединения непересекающихся множеств 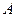и 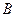, т.е. 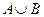. Элементы множества 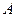получат номера от 1 до 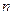. Множества 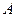и 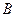не содержат одинаковых элементов, поэтому элементы множества 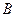получат номера от 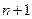до 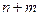. При помощи этой процедуры подсчета элементов множества 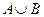все они будут исчерпаны, следовательно, множество 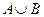содержит 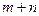элементов.

Замечание: Правило сложения, как и правило умножения, можно обобщить на случай 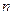слагаемых.

Можно также отметить, что знак умножения в соответствующем правиле соответствует союзу «и» русского языка. А знак сложения – союзу «или». Причём, союз «или» применяется во взаимоисключающем смысле.

Для дальнейшего изложения необходимо ввести следующее вспомогательное понятие.

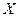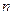Определение 1: Пусть дано конечное множество из элементов. Всякий набор из 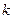элементов данного множества (при этом элементы в наборе могут и повторяться) будем называть 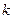- расстановками.

Через понятие расстановки вводятся основные определения комбинаторики: сочетания, размещения и перестановки. При этом каждое из этих понятий может быть с повторениями и без повторений.