Для проверки статистических гипотез применяют критерии согласия, т.е. правила, позволяющие принять или отвергнуть выдвинутую гипотезу. Так как нормальное распределение встречается довольно часто, то наиболее часто проверяют гипотезу о соответствии выборочного распределения нормальному. Из множества критериев согласия о распределениях наиболее мощным является критерий c2 Пирсона (критерий «хu-квадрат» Пирсона).
Пусть в результате 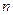 наблюдений получено статистическое распределение выборки:
наблюдений получено статистическое распределение выборки:
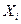
| 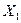
| 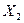
| … | 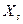
|
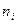
| 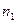
| 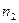
| … | 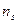
|
Выдвинем статистическую гипотезу: «Генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение».
Критерий Пирсона представляет собой следующее правило:
Для того, чтобы проверить гипотезу о нормальном распределении генеральной совокупности, необходимо:
1. Вычислить выборочную среднюю 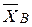 и выборочное среднее квадратическое отклонение
и выборочное среднее квадратическое отклонение 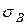 ;
;
2. Вычислить теоретические частоты 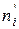 формуле:
формуле: 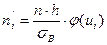 ,
,
где 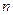 -объем выборки,
-объем выборки,
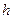 - шаг (разность между двумя соседними равноотстоящими вариантами),
- шаг (разность между двумя соседними равноотстоящими вариантами),
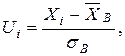
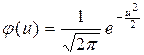 (находят по таблице - приложение 1)
(находят по таблице - приложение 1)
3. Вычислить наблюдаемое значение критерия 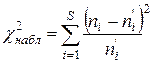
4. Вычислить число степеней свободы 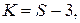 где S - число групп, на которые разбита выборка;
где S - число групп, на которые разбита выборка;
5. Выбрать уровень значимости 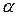 ;
;
6. По таблице критических точек распределения 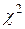 найти критическую точку
найти критическую точку
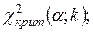

7. Если 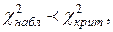 , то нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности, т.е. эмпирические и теоретические частоты различаются незначимо (случайно).
, то нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности, т.е. эмпирические и теоретические частоты различаются незначимо (случайно).
8. Если 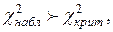 то гипотезу о нормальном распределении генеральной совокупности отвергают, т.е. эмпирические и теоретические частоты различаются значимо.
то гипотезу о нормальном распределении генеральной совокупности отвергают, т.е. эмпирические и теоретические частоты различаются значимо.
 2015-03-27
2015-03-27 543
543








