Основные элементарные функции.
1) 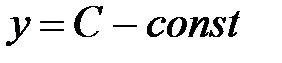 (постоянная) (рис. 1). Область определения
(постоянная) (рис. 1). Область определения 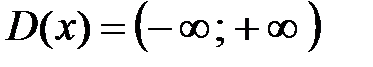 .
.
2) 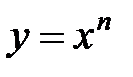 – степенная функция.
– степенная функция.
а) 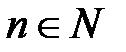 . Область определения
. Область определения 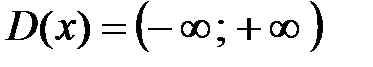 (рис. 2, 3).
(рис. 2, 3).
б) 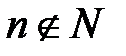 .
.
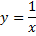 Рис.4
Рис. 56
Рис.4
Рис. 56
|
при
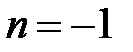
– гипербола
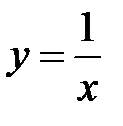
. Область определения
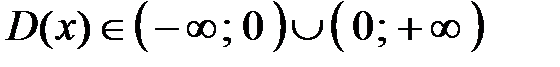
(рис. 4).
при 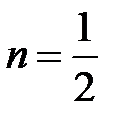 -
- 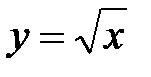 . Область определения
. Область определения 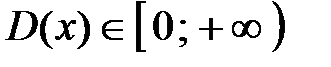 (рис. 4).
(рис. 4).
3) 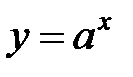 – показательная функция. Область определения:
– показательная функция. Область определения: 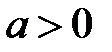 ,
, 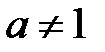 ,
, 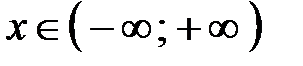 (рис. 5). Если
(рис. 5). Если 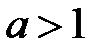 , функция возрастает, если
, функция возрастает, если 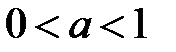 , функция убывает.
, функция убывает.
4)
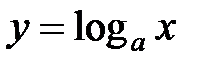
– логарифмическая функция. Область определения:
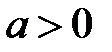
,
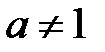
,
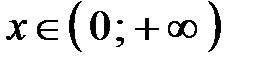
(рис. 6). Если
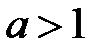
, функция возрастает, если
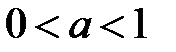
, функция убывает.
5) Тригонометрические функции:
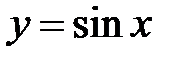 . Область определения:
. Область определения: 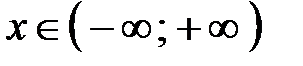 , период
, период 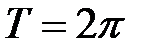 .
.
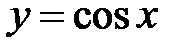 . Область определения:
. Область определения: 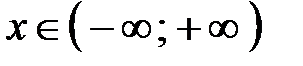 , период
, период 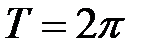 .
.
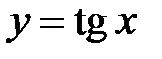 . Область определения:
. Область определения: 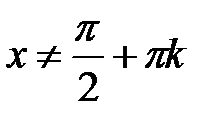 ,
, 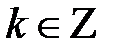 (точки разрыва). Период
(точки разрыва). Период 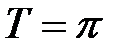 (рис. 8).
(рис. 8).
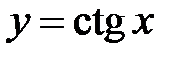 . Область определения:
. Область определения: 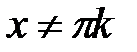 ,
, 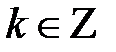 (точки разрыва). Период
(точки разрыва). Период 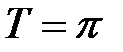 (рис. 9).
(рис. 9).
 Рис.7
Рис. 7
Рис.7
Рис. 7
|
 Рис. 8 Рис. 8
|
 Рис. 9
Рис. 9
|
Рассмотрим две функции 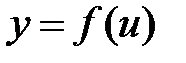 и
и 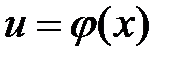 .
.
Определение. Функция 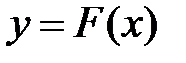 , заданная по правилу: каждому
, заданная по правилу: каждому 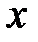 ставится в соответствие
ставится в соответствие 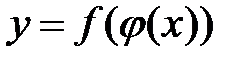 , называется сложной функцией относительно переменной
, называется сложной функцией относительно переменной 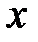 ,
, 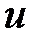 при этом называется промежуточным аргументом сложной функции.
при этом называется промежуточным аргументом сложной функции.
Определение. Функции,построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа образования сложной функции, называются элементарными.
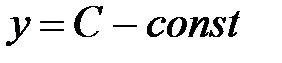 (постоянная) (рис. 1). Область определения
(постоянная) (рис. 1). Область определения 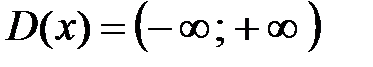 .
.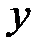
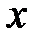


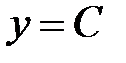
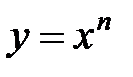 – степенная функция.
– степенная функция.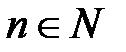 . Область определения
. Область определения 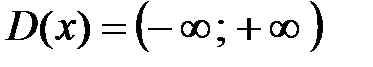 (рис. 2, 3).
(рис. 2, 3).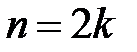
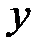
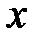

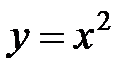
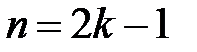
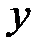
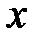

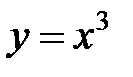
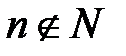 .
.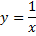 Рис.4
Рис. 56
Рис.4
Рис. 56
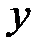
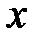
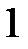
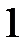

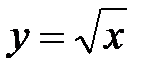
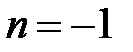 – гипербола
– гипербола 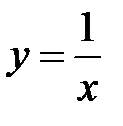 . Область определения
. Область определения 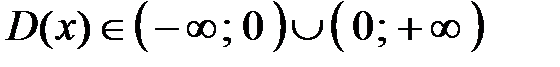 (рис. 4).
(рис. 4).
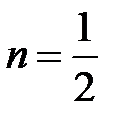 -
- 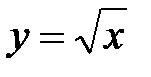 . Область определения
. Область определения 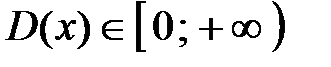 (рис. 4).
(рис. 4).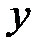
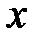
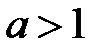
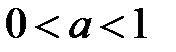
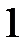

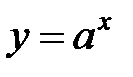 – показательная функция. Область определения:
– показательная функция. Область определения: 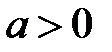 ,
, 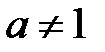 ,
, 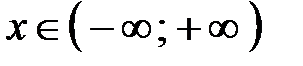 (рис. 5). Если
(рис. 5). Если 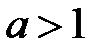 , функция возрастает, если
, функция возрастает, если 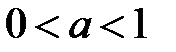 , функция убывает.
, функция убывает.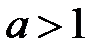
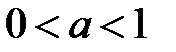
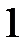
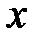
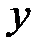

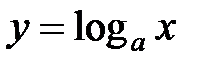 – логарифмическая функция. Область определения:
– логарифмическая функция. Область определения: 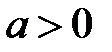 ,
, 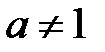 ,
, 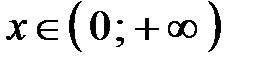 (рис. 6). Если
(рис. 6). Если 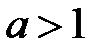 , функция возрастает, если
, функция возрастает, если 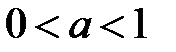 , функция убывает.
, функция убывает.
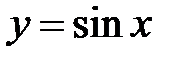 . Область определения:
. Область определения: 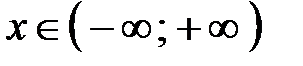 , период
, период 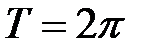 .
.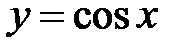 . Область определения:
. Область определения: 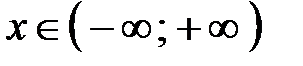 , период
, период 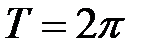 .
.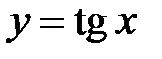 . Область определения:
. Область определения: 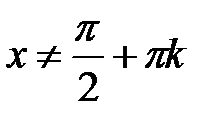 ,
, 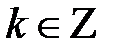 (точки разрыва). Период
(точки разрыва). Период 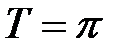 (рис. 8).
(рис. 8).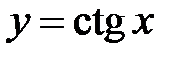 . Область определения:
. Область определения: 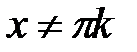 ,
, 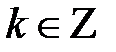 (точки разрыва). Период
(точки разрыва). Период 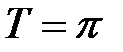 (рис. 9).
(рис. 9).
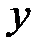

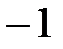
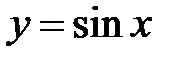
 Рис.7
Рис. 7
Рис.7
Рис. 7
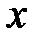
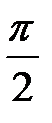
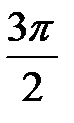
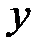

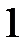
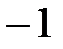
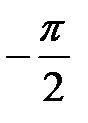
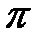
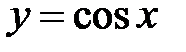
 Рис. 8
Рис. 8
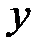
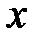

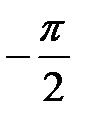
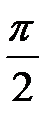
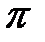
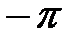
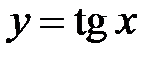
 Рис. 9
Рис. 9
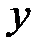

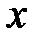
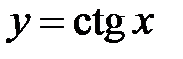
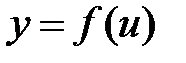 и
и 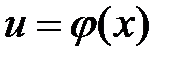 .
.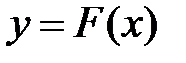 , заданная по правилу: каждому
, заданная по правилу: каждому 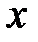 ставится в соответствие
ставится в соответствие 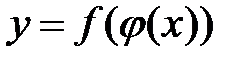 , называется сложной функцией относительно переменной
, называется сложной функцией относительно переменной 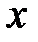 ,
, 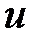 при этом называется промежуточным аргументом сложной функции.
при этом называется промежуточным аргументом сложной функции. 2015-03-27
2015-03-27 276
276







