Задача №1

Функция полезности растёт по своим аргументам, поэтому лишних долларов у Данилы не останется. Если он пойдёт в парк, то 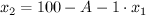. Если не пойдёт, то 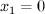, а 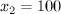. В каком случае будет больше полезность, тот и надо выбрать. Во втором случае всё просто: 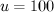, а в первом ещё надо выбрать оптимальные 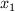и 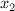. Найдём оптимальный 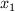, максимизируя 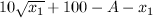. Приравняв первую производную к нулю, получим 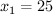. Прикинув, как выглядит график функции, убедимся, что мы нашли максимум, а не минимум. Кто не уверен, можно проверить, что вторая производная в точке оптимума отрицательна.
Подставим в функцию полезности: 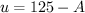. Если 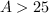, то это меньше 100, и значит, Мирснейленд останется без Данилы.

Ответ: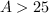

ЗАДАЧА №2 Еdp=0,75/15=0,05