ЗАНЯТИЯ 7, 8. Трапеция.
В классе:
1. Высота и диагональ равнобедренной трапеции равны 5 и 13. Найти площадь этой трапеции. Ответ: 60.
2. В равнобедренной трапеции диагональ перпендикулярна боковой стороне. Найдите площадь этой трапеции, если длины ее боковой стороны и высоты равны 20 и 12 соответственно. Ответ: 108.
3. Найти площадь трапеции, если ее высота равна 4, диагонали перпендикулярны, а одна из них равна 5. Ответ: 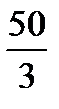 .
.
4. Основания трапеции равны 10 и 24, а ее боковые стороны равны 13 и 15. Найти площадь этой трапеции. Ответ: 204.
5. Основания трапеции равны 1 и 11. Прямая, параллельная основаниям трапеции, делит ее площадь в отношении 2:3, считая от меньшего основания. Найти длину отрезка этой прямой, заключенного между боковыми сторонами трапеции.
Ответ: 7.
6. В прямоугольной трапеции большая диагональ равна 24 и является биссектрисой острого угла. Найти площадь этой трапеции, если расстояние от вершины ее тупого угла до диагонали
равно 9. Ответ 246,24.
7. Биссектрисы тупых углов при основании трапеции пересекаются на другом ее основании. Найти стороны трапеции, если ее высота равна 12, а длины биссектрис равны 15 и 13.
Ответ: 14, 12,5, 29,4, 16,9.
8. Диагонали разбивают трапецию на 4 треугольника. Площади треугольников, прилегающих к основаниям, равны 4 и 9. Найти площади треугольников, прилегающих к боковым сторонам. Ответ: 6.
9. Около окружности радиуса 2 описана равнобедренная трапеция с площадью 20. Найти стороны этой трапеции. Ответ: 2, 8, 5, 5.
10. Расстояния от концов боковой стороны трапеции до центра вписанной в нее окружности равны 4 и 8. Найти среднюю линию этой трапеции. Ответ: 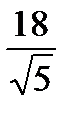 .
.
11. Трапеция ABCD с основаниями AD и ВС вписана в окружность радиуса 8. Найти среднюю линию этой трапеции, если 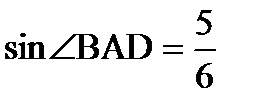 и
и 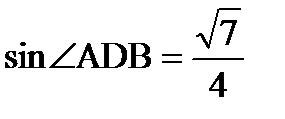 . Ответ: 10.
. Ответ: 10.
12. Окружность, построенная на основании AD трапеции ABCD как на диаметре, проходит через середины боковых сторон АВ и CD трапеции и касается основания ВС. Найти углы трапеции. Ответ: 750, 750, 1050, 1050.
Дома:
1. Найти площадь трапеции, если ее основания равны 6 и 11, одна из боковых сторон равна 4, а сумма углов при большем основании равна 900. Ответ 20,4.
2. В трапеции ABCD боковая сторона AD перпендикулярна основаниям, а диагональ BD является биссектрисой острого угла. Найдите площадь этой трапеции, если AD=24 и CD=25. Ответ: 684.
3. Найти площадь трапеции диагонали которой равны 7 и 8, а основания равны 3 и 6.
Ответ: 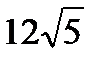 .
.
4. Средняя линия трапеции равна 10 и делит площадь в отношении 3:5. Найти основания этой трапеции. Ответ: 5 и 15.
5. На боковых сторонах АВ и CD трапеции ABCD взяты точки Р и Q соответственно, причем АР:РВ=2:3. Отрезок PQ разбивает трапецию на части, одна из которых по площади втрое больше другой. Найти отношение CQ:QD, если AD=2BC. Ответ: 3:29.
6. В равнобедренной трапеции диагональ делит острый угол пополам. Периметр трапеции равен 132, а ее основания относятся как 2:5. Найти стороны этой трапеции. Ответ: 24, 24, 24, 60.
7. Через точку пересечения диагоналей трапеции проведена прямая, параллельная основаниям. Отрезок этой прямой, заключенный между боковыми сторонами трапеции, равен 2. Найти основания этой трапеции, если их отношение равно 4.
Ответ: 5 и 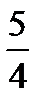 .
.
8. В трапеции ABCD длины оснований AB и CD относятся как 5:1, а площадь этой трапеции равна 32. Точки M и N являются серединами боковых сторон AD и BC. Отрезки AN и BM пересекаются в точке K, а отрезки CM и DN пересекаются в точке L. Найти площадь четырехугольника MKNL. Ответ: 9.
9. В прямоугольную трапецию с основаниями 2 и 3 вписана окружность. Найти ее радиус.
Ответ: 1,2.
10. Средняя линия равнобедренной трапеции равна 5. Она делит трапецию на части, отношение площадей которых равно 7:13. Найти площадь этой трапеции, если в нее можно вписать окружность. Ответ: 20.
11. Четырехугольник ABCD вписан в окружность с центром О, причем ÐВОА=ÐCOD=600. Перпендикуляр ВК, опущенный из вершины В на сторону AD, равен 6. Сторона ВС в три раза меньше стороны AD. Найти площадь треугольника COD. Ответ: 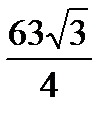 .
.
12. Окружность, построенная на основании ВС трапеции ABCD как на диаметре, проходит через середины диагоналей АС и BD трапеции и касается основания AD. Найти углы трапеции. Ответ: 300, 300, 1500, 1500.
ЗАНЯТИЕ 9. Параллелограмм и ромб.
В классе:
1. В параллелограмме ABCD диагональ BD перпендикулярна стороне AB. Найдите AD, если 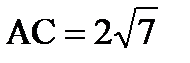 и AB=2. Ответ: 4.
и AB=2. Ответ: 4.
2. Найти площадь параллелограмма, если его диагонали равны 3 и 5, а острый угол равен 600. Ответ: 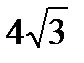 .
.
3. Периметр параллелограмма равен 90, а его острый угол равен 600. Диагональ делит острый угол в отношении 1:3. Найти длины диагоналей этого параллелограмма. Ответ15 и 30.
4. Найдите меньшую диагональ ромба с площадью 3 и высотой 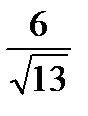 . Ответ: 2.
. Ответ: 2.
5. Найти углы ромба, если площадь вписанного в него круга в 2 раза меньше площади самого ромба. Ответ: 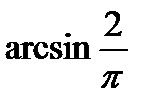 и
и 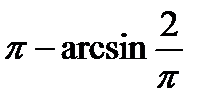 .
.
6. Дан ромб ABCD. Окружность радиуса R описана около треугольника ABD и проходит через центр окружности вписанной в треугольник BCD. Найти площадь ромба. Ответ: 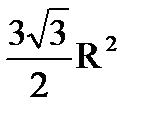 .
.
7. В ромб вписан круг, а в круг вписан квадрат. Найти углы ромба если площадь квадрата в 4 раза меньше площади ромба. Ответ: 300 и 1500.
Дома:
1. В параллелограмме ABCD биссектриса тупого угла при вершине B пересекает сторону AD в точке F. Найти периметр параллелограмма, если AB=12, AF:FD=4:3. Ответ 66.
2. В параллелограмме одна из сторон равна 7, а одна из диагоналей равна 13. Найти вторую сторону этого параллелограмма, если она на 5 меньше второй диагонали. Ответ: 16.
3. В параллелограмме острый угол равен 450, а расстояния от точки пересечения диагоналей до неравных сторон равны 2 и 3. Найти площадь этого параллелограмма. Ответ: 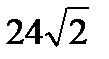 .
.
4. Найдите площадь ромба с тупым углом 1200 и большей диагональю 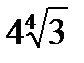 .Ответ: 8.
.Ответ: 8.
5. Длины меньшей диагонали, стороны и большей диагонали ромба образуют геометрическую прогрессию. Найти углы этого ромба. Ответ: 300 и 1500.
ЗАНЯТИЕ 10. Прямоугольник и квадрат.
В классе:
1. В квадрат с площадью 18 вписан прямоугольник так, что на каждой стороне квадрата лежит вершина прямоугольника. Найти площадь прямоугольника, если его стороны относятся как 1:2. Ответ: 8.
2. В прямоугольном треугольнике ABC расположен прямоугольник KLMN так, что сторона KL лежит на гипотенузе BC, а вершины M и N лежат на катетах AB и AC соответственно, причем AB=4 и AC=3. Найти стороны прямоугольника, если его площадь равна 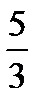 , а периметр
, а периметр
меньше 9. Ответ: 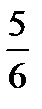 и 2.
и 2.
3. Точка M делит диагональ AC квадрата ABCD со стороной a в отношении AM:MC=3:1. Точка N лежит на стороне AB, причем ÐNMD – прямой. Найти AN. Ответ: 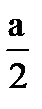 .
.
4. В квадрате ABCD со стороной a точки E и F являются серединами сторон AB и CD. Точка K лежит на отрезке CF, а точка N лежит на отрезке AD, причем отрезки EF и KN пересекаются в точке M. Найти площадь треугольника KFM, если CK:KF=1:5, а площадь трапеции EMNA относится к площади самого квадрата как 3:10. Ответ: 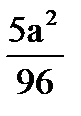 .
.
Дома:
1. В полукруге радиуса 5 расположен прямоугольник ABCD сторона AB которого лежит на диаметре полукруга, а вершины C и D лежат на полуокружности. Найти стороны прямоугольника, если его площадь равна 24, а диагональ больше 8. Ответ: 3 и 8.
2. В прямоугольнике ABCD на сторонах AB=6 и BC=8 взяты точки M и N так, что прямые AC и MN параллельны. Периметр многоугольника AMNCD относится к периметру треугольника MNB как 7:3. Найти MN. Ответ: 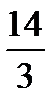 .
.
3. На стороне NP квадрата MNPQ взята точка A, а на стороне PQ взята точка B так, что NA:AP=PB:BQ=2:3. Отрезки MA и NB пересекаются в точке L. Найти отношение AL:LM. Ответ: 4:25.
 2015-03-07
2015-03-07 1769
1769








