Свойства и признаки равнобедренной трапеции

· Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции.

· Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований

· Углы при любом основании равны.

· Длины диагоналей равны.

· Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Площадь трапеции равна произведения полусуммы её оснований на высоту.

В случае, есл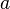и и 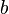— основания и 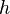— высота, формула площади:

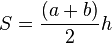
В случае, если 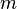— средняя линия и 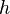— высота, формула площади:

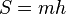
* Приведённые выше две формулы эквивалентны, так как полусумма оснований равняется средней линии трапеции:

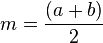
Формула, где 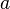, 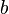— основания, и 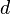— боковые стороны трапеции:

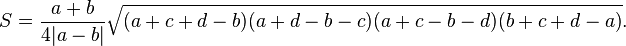
Площадь равнобедренной трапеции с радиусом вписанной окружности, равным , и углом при основании :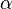

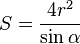
Площадь равнобедренной трапеции:

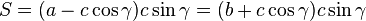
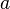где - боковая сторона, - большее основание, 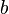- меньшее основание, 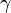- угол между большим основанием и боковой стороной.

Средняя линия трапеции параллельна основаниям и равна их полусумме.