| Номер интервала, i | Начало интервала Xi, мм | Конец интервала Xi+1, мм | Середина интервала Xi | Частота mi | Частность 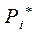
| Плотность
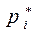 , мм-1 , мм-1
|
| 8,911 8,913 8,915 8,917 8,919 8,921 8,923 8,925 | 8,913 8,915 8,917 8,919 8,921 8,923 8,925 8,927 |
6. Определить среднее арифметическое 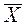 ряда наблюдений и точечную оценку среднего квадратичного отклонения Sx
ряда наблюдений и точечную оценку среднего квадратичного отклонения Sx
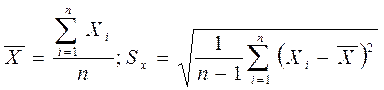 , (6)
, (6)
которые принимают в качестве параметров нормального теоретического распределения с плотностью px(x).
7. Для каждого интервала находят вероятности попадания в них результатов наблюдений
либо по общей формуле
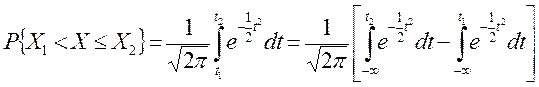 (7)
(7)
С помощью функции Ф(z) вероятность, определенную по формуле (7), находят как 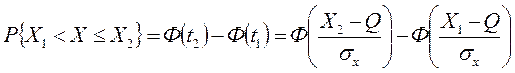 (8)
(8)
либо приближенно как произведение плотности теоретического распределения в середине интервала на его длину
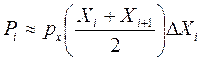 (9)
(9)
Плотности нормированного нормального распределения p(ti) находят по табл. 1 прил. 2. Экстраполяция значения ti.
8. Для каждого интервала вычислить величины 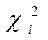 (i = 1, 2,…, r) и суммируют их по всем i, в результате чего получают меру распределения
(i = 1, 2,…, r) и суммируют их по всем i, в результате чего получают меру распределения 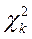 .
.
9. Определяют число степеней свободы k = r - 3 и, задаваясь уровнем значимости q = 1 - a; a = 0,9, найти по табл. 3 прил. 2 значения 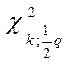 и
и 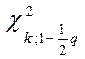 . Если
. Если 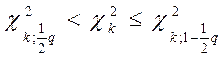 , то распределение результатов наблюдений считают нормальным.
, то распределение результатов наблюдений считают нормальным.
10. Заполнить таблицу результатов вычислений (табл. 2).
СОДЕРЖАНИЕ ОТЧЕТА
Отчет должен содержать:
1. Наименование работы.
2. Цель работы.
3. Гистограмму и кривую распределения результатов измерений.
4. Таблицы наблюдений и вычислений.
5. Заключение о работе.
Таблица 2
 2015-03-08
2015-03-08 273
273








