Построение конечных автоматов
ЦЕЛЬ РАБОТЫ
14.1.1 Ознакомиться с теоретическими сведениями.
14.1.2 Получить практические навыки по построению конечных автоматов.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
14.2.1 Методические указания по выполнению практической работы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
14.3.1 Изучить методические указания к практической работе.
14.3.2 В соответствии с полученным вариантом постройте конечный автомат.
СОДЕРЖАНИЕ ОТЧЕТА
14.4.1 Цель работы
14.4.2 Методические рекомендации
14.4.3 Порядок выполнения работы
14.4.4 Ответы на контрольные вопросы
14.4.5 Выводы
КОНТРОЛЬНЫЕ ВОПРОСЫ
14.5.1 Что называется конечным автоматом Мили?
14.5.2 Что называется конечным автоматом Мура?
14.5.3 Назовите объекты конечного автомата?
14.5.4 Что называется функцией изменения состояний (функцией переходов)?
14.5.5 Что называется выходной функцией?
14.5.6 Какими способами можно представить конечный автомат?
ПРИЛОЖЕНИЕ 1
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Конечный автомат определяется как совокупность следующих пяти объектов:
1) S – конечное множество состояний;
2) I – конечное множество входных символов;
3) О – конечное множество выходных символов;
4) s - отображение S´I в S; эта функция определяет по текущему состоянию и входу следующее состояние и называется функцией изменения состояний или функцией переходов;
5) d - отображение S´I в О; эта функция определяет по текущим состоянию и входу текущее значение выхода и называется выходной функцией.
Если d зависит как от S, так и от I, то конечный автомат называется автоматом Мили; если же d зависит только от S, - то автомат Мура. В автомате Мура, в отличие от автомата Мили, каждый выходной символ формируется просто по состоянию автомата, а входные символы при этом не учитываются.
Пример 1. Рассмотрим конечный автомат М, на вход которого поступают последовательно пары компонент двоичных представлений чисел x и y (начиная с младших разрядов), а на выходе последовательно (начиная с младших разрядов) формируется двоичное представление суммы х+y.
Пусть х1, х2, …, хi, y1, y2, …, yi, …, s1, s2, …, si,… - двоичные представления чисел х, y и х+у соответственно (начиная с младших разрядов). Пусть с0 = 0 и сi – символ переноса из (i - 1)-го разряда в i-й разряд. Тогда,
si = xiÅyiÅci, ci+1 = Maj3 (xi, yi, ci).
Таким образом, если в качестве состояния, которое запоминается после введения в конечный автомат i-1 разрядов двоичных представлений, взять величину сi, то можно правильно вычислить как входной символ si, так и следующее состояние. Обозначим через t1 и t2 состояния конечного автомата, соответствующие сi = 0 и сi = 1. Пусть I ={(0,0), (0, 1), (1, 0), (1, 1)}, O={0, 1}. Функция d, s определяются табл. 1, которая называется таблицей переходов и выходных значений. Рассмотренный конечный автомат является автоматом Мили и называется последовательным двоичным сумматором.
Таблица 1
Таблица переходов и выходных значений
| Состояние конечного автомата | (0, 0) | (0, 1) | (1, 0) | (1, 1) |
| t1 | t1, 0 | t1, 1 | t1, 1 | t2, 0 |
| t2 | t1, 1 | t2, 0 | t2, 0 | t2, 1 |
Диаграмма состояний (диаграмма изменения состояний) G(M) конечного автомата М = (S, I, O, s, d) определяется следующим образом. Между вершинами и состояниями из S устанавливается взаимно однозначное соответствие; при этом каждой вершине присваивается имя соответствующего ей состояния. Вершина с именем s обычно называется просто вершиной s. Из каждой вершины s проводится ориентированные ребра во все вершины s(s, a), aÎI. Ребру, проведенному из вершины s в вершину s(s, a), присваивается имя a/[d(s, a)]. Других ребер диаграмма состояний G(M) не имеет.
Пример 2. На рис. 1 приведена диаграмма состояний конечного автомата, описанного в примере 1. Вместо того чтобы проводить i ребер с совпадающими начальными и совпадающими конечными точками, но различными именами, на диаграмме состояний для просторы проводиться только одно ребро, на котором указываются все i имена.
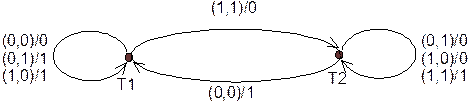 |
Рис.1.
ПРИЛОЖЕНИЕ 2
 2015-03-08
2015-03-08 220
220






