Отношения между суждениями по значениям истинности

Суждения, как и понятия, делятся на сравнимые (имеют об­щи субъект или предикат) и несравнимые. Сравнимые суждения делятся на совместимые и несовместимые.

В математической логике два высказывания р и q называ­йся несовместимыми, если из истинности одного из них необходимо следует ложность другого (т. е.р и q никогда не могут казаться одновременно истинными). “Это понятие легко распространить на любое число высказываний: высказывания р_1,p₂... р₁₁ называются несовместимыми, если не может оказаться, что все они являются одновременно истинными”'.

Совместимые выражают одну и ту же мысль полностью или лишь в некоторой части. Отношения совместимости: эквивалентность, логическое подчинение, частичное совпадение (субконтрарность). Совместимые эквивалентные суждения выражают одну и ту же мысль в различной форме (“Юрий Гагарин - первый космонавт” и “Юрий Гагарин первым полетел в космос”). Субъект здесь один и тот же, а предикаты различные по форме, но одинаковые по смыслу. В двух эквивалентных суждениях “Михаил Шолохов-лауреат Нобелевской премии” и “Автор романа “Тихий Дон” -лауреат Нобелевской премии” одинаковыми являются предикаты, а различными по форме выражения, но тождественными понятиями -субъекты.

Если два высказывания эквивалентны, то невозможно, чтобы одно из них было истинным, а другое ложным.

В сочинении, при заучивании материала, в устном изложении текста, при переводе с одного языка на другой - всюду требуется умение кратко и корректно излагать свои мысли.

Совместимые суждения, находящиеся в отношении логического подчинения, имеют общий предикат; понятия, выражающие субъекты двух таких суждений, также находятся в отношении логического подчинения. Отношения между суждениями по истинности принято схематически изображать в виде “логического квадрата” (рис. 17).

_____________________

'Кемени Д., Снелл Д., Томпсон Д.. Введение в конечную математику. // Пер. с англ.. М.,1963. С.50.

Возьмем суждение “Все слоны – млекопитающие”. Это суждение А общеутвердительное (подчиняющее). Суждение! - “Неко­торые слоны - млекопитающие” - подчиненное.

Для суждений А и I, а также Е и О, находящихся в отноше­нии логического подчинения, истинность общего суждения оп­ределяет истинность частного, подчиненного суждения. Но ло­жность общего суждения оставляет частное суждение неопре­деленным.

Противоположность (контрарность)

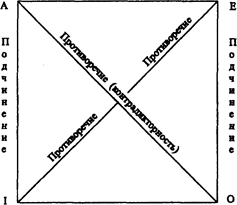
Субконтрарность.

Рис.17

Истинность частного суждения оставляет общее суждение неопределенным (при нарушении этого правила может возник­нуть логическая ошибка - “поспешное обобщение”). Ложность частного суждения обусловливает ложность общего суждения. Если истинно суждение “Ни одна хлорелла не является много­клеточной зеленой водорослью”, то будет истинным и суждение “Некоторые хлореллы не являются многоклеточными зелены­ми водорослями”. Умозаключение от общего суждения к логи­чески подчиненному ему частному суждению всегда будет да­вать истинное заключение.

В отношении частичного совпадения (субконтрарности) находятся два таких совместимых суждения I и О, которые

имеют одинаковые субъекты и одинаковые предикаты, но раз­личаются по качеству. Например, (I) “Некоторые свидетели дают истинные показания” и (О) “Некоторые свидетели не дают истинных показаний”. Оба они одновременно могут быть ис­тинными, но не могут быть одновременно ложными. Если одно из них ложно, то другое обязательно истинно. Но если одно из них истинно, то другое неопределенно (оно может быть либо истинным, либо ложным). Например, если истинно суждение (I) “Некоторые книги этой библиотеки изданы на корейском язы­ке”, то суждение (О) “Некоторые книги этой библиотеки не яв­ляются изданными на корейском языке” будет неопределенным, т.е. оно может быть как истинным, так и ложным.

Отношения несовместимости: противоположность, проти­воречие. По “логическому квадрату” в отношении противополож­ности (контрарности) находятся суждения А и Е. Два суждения: (А) “Все люди трудятся добросовестно” и (Е) “Ни один человек не трудится добросовестно” - оба ложны. Но А и Е не могут быть оба истинными. Если одно из противоположных суждений истинно, то другое будет ложным.

Итак, из истинности одного из противоположных суждений вытекает ложность другого, но ложность одного из них оставля­ет другое суждение неопределенным.

В отношении противоречия (контрадикторности) находят­ся суждения А и О, а также Е и I. Два противоречащих сужде­ния не могут быть одновременно истинными и одновременно ложными. Если в настоящее время истинно суждение (I) “Неко­торые летчики - космонавты”, то ложным будет суждение (Е) “Ни один летчик не является космонавтом”.

Закономерности, выражающие отношения между суждениями по истинности, имеют большое познавательное значение, так как они помогают избежать ошибок при непосредственных умозак­лючениях, производимых из одной посылки (одного суждения).