Рассуждение по правилу введения импликации

Правило вывода сформулировано так:

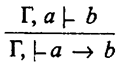Данное правило читается так: “Если из посылок гамма (Г) и посьшки а выводится заключение b, то из одних посылок Г вы­водится, что а имплицирует b ”. Это правило вывода имеет так­же название “теоремы о дедукции”. Здесь “Г” может быть и пустым множеством посылок. Приведем пример рассуждения человека, поясняющий приведенное правило. Пусть Г содержит следующие посылки: 1) “Я купил автомобиль”; 2) “Я получил права водителя”; 3) “Я имею свободное время”. Посылка a означает: “Я имею деньги”. Заключение b означает: “Я поеду в туристическое путешествие с семьей на автомобиле”. То, что записано над чертой, будет содержательно прочитано так: “Если я купил автомобиль, получил права водителя, имею свободное время и у меня есть деньги, то из этого последует заключение:

“Я поеду в туристическое путешествие с семьей на автомоби­ле”. То, что записано под чертой содержательно можно прочи­тать так: “Я купил автомобиль, получил права водителя, имею свободное время”. Отсюда следует заключение: “Если я буду иметь деньги, то я поеду в туристическое путешествие с семь­ей на автомобиле”.

2. Правило сведения “к абсурду”

Это так называемое reductio ad absurdum - метод доказатель­ства приведением к нелепости, иначе это называется правилом введения отрицания. Оно записывается так:

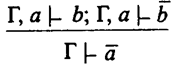Правило читается так: “Если из посылок Г и посылки а вы­водится противоречие, т. е. b и не-b, то из одних Г выводится не-а”. Метод сведения к абсурду широко применяется в мыш­лении, как научном, так и в обыденном.

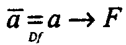В классической двузначной логике метод сведения к абсур­ду выражается в виде формулы:

где F- противоречие или ложь. Эта формула говорит о том, что суждение а надо отрицать (считать ложным), если из а вытека­ет противоречие.

Определение отрицания посредством сведения к абсурду, про­тиворечию широко используется не только в классической, но и в неклассических логиках: в многозначных, конструктивных и интуиционистской.