Решение. Каждый из зарядов создают в точке А напряженность электрического поля E1 и Е2 и потенциалы электрического поля φ1 и φ2 по принципу суперпозиции

Каждый из зарядов создают в точке А напряженность электрического поля E₁ и Е₂ и потенциалы электрического поля φ₁ и φ₂ по принципу суперпозиции полей.

Результирующая напряженность равна 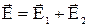(1), а потенциал 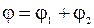, где величина напряженности электрического поля точечного заряда равна соответственно: 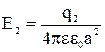, а потенциалы: 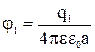и 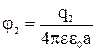. Тогда результирующий потенциал в точке А равен: 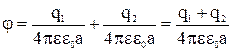. (2) Результирующую напряженность найдем по теореме косинусов . Проверим формулу (2) по размерности величин:

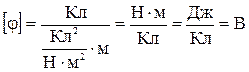. Подставим значение величин и вычислим искомую величину потенциала и напряженности:

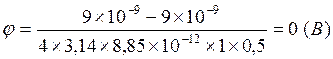
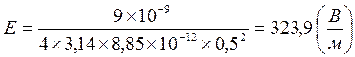
Ответ: ;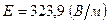

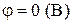
Вывод: Так как |q₁| = |q₂|, а расстояние между зарядами и от зарядов до исследуемой точки одинаково, то E₁ = E₂ и |φ₁| = |φ₂|, следовательно результирующая величина напряженности равна Е = Е₁, а результирующий потенциал φ = 0.

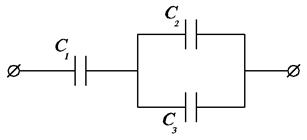
Пример № 3. Три конденсатора емкостями С₁=1мкФ, С₂=1мкФ и С₃=2мкФ соединены по схеме (рис.1.,а) и подключены к источнику постоянного напряжения 120 В. Какова емкость батареи? Определить заряд и напряжение на конденсаторе С₁.

Дано:

С₁=1мкФ=10^-6Ф

С₂=1мкФ=10^-6Ф

С₃=2мкф=2∙10^-6Ф

U=120В

C-? q-? U₁-?