Электрон в водородоподобном атоме двигается по круговой орбите, поэтому кулоновская сила взаимодействия электрона и ядра является центростремительной силой, то есть
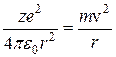 ,
,
где z – номер элемента, е – заряд электрона, 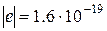 Кл, r – радиус орбиты, u – скорость электрона на орбите, e0 – электрическая постоянная, m – масса электрона, m=9,110-31 кг.
Кл, r – радиус орбиты, u – скорость электрона на орбите, e0 – электрическая постоянная, m – масса электрона, m=9,110-31 кг.
По второму постулату Бора момент импульса электрона на любой орбите удовлетворяет условие: 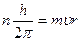 ,
,
где n – номер орбиты, h – стала Планка, h=6.6310-34 ×Дж·с, r, u – соответственно радиус орбиты и скорость электрона на ней.
Решим систему уравнений:
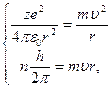
разделим первое уравнение на второе и получим:
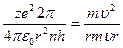 или
или 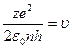 ,
,
по условию задачи z=2, n=1.
Соответственно:
u = 
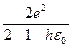 =
= 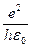 ,
,
рассчитаем:
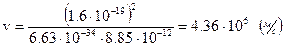 .
.
По второму постулату Бора определим радиус орбиты:
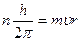 .
.
Соответственно:
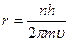 , если n=1, то
, если n=1, то 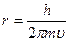 ,
,
рассчитаем:
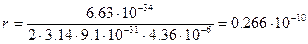 (м).
(м).
Ответ: 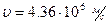 ,
, 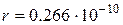 м.
м.
Пример № 2. Определить, какое количество ядер радиоактивного препарата 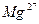 , взятого в количестве 0,2мг, распадается в течение: а) 2с; б) 1ч.
, взятого в количестве 0,2мг, распадается в течение: а) 2с; б) 1ч.
Дано:
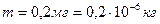 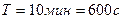 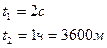 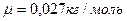 | Решение: Число нераспавшихся радиоактивных ядер 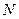 за время за время  вычисляется по формуле: вычисляется по формуле: 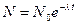 , (1) где , (1) где 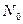 - исходное число ядер в момент времени t=0; - исходное число ядер в момент времени t=0; 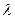 - постоянная радиоактивного распада. - постоянная радиоактивного распада. |
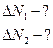 | Тогда число распавшихся ядер за время  будет равно: будет равно: 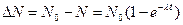 (2) (2) |
Постоянная радиоактивного распада связана с периодом полураспада Т соотношением: 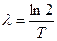 . Число радиоактивных ядер в данной массе вещества вычисляется с помощью закона Авогадро:
. Число радиоактивных ядер в данной массе вещества вычисляется с помощью закона Авогадро: 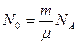 , (3)
, (3)
где 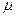 - масса одного моля;
- масса одного моля; 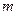 -масса вещества;
-масса вещества; 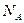 - число Авогадро.
- число Авогадро.
С учетом значения 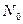 и
и 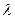 формула (2) примет вид:
формула (2) примет вид: 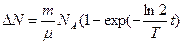 (4).
(4).
Если время распада t значительно меньше периода полураспада Т(t<<T), получим: 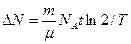 (5). Число распавшихся за время распада
(5). Число распавшихся за время распада  ядер вычисляется по формуле (5). Подставим числовые данные и определим
ядер вычисляется по формуле (5). Подставим числовые данные и определим 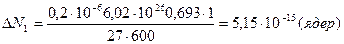 . Для второго промежутка времени
. Для второго промежутка времени 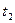 нельзя применить приближенную формулу (5), так как
нельзя применить приближенную формулу (5), так как 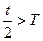 , поэтому вычисление распавшегося числа атомов произведем по формуле (4):
, поэтому вычисление распавшегося числа атомов произведем по формуле (4):
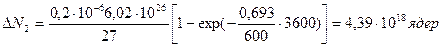
Ответ: 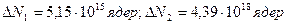
Пример № 3. Вычислить дефект массы и энергию связи ядра 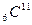 .
.
Дано:
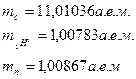 | Решение: Масса ядра всегда меньше суммы масс свободных протонов и нейтронов, из которых состоят ядра. |
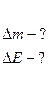 | Дефект массы ядра 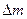 определяется разностью суммы масс свободных нуклонов (протонов и нейтронов) и массой ядра: определяется разностью суммы масс свободных нуклонов (протонов и нейтронов) и массой ядра: 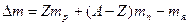 , (1) , (1) |
где 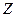 - порядковый номер элемента (число протонов в ядре); А – массовое число (число нуклонов в ядре);
- порядковый номер элемента (число протонов в ядре); А – массовое число (число нуклонов в ядре); 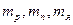 – соответственно масса протона, нейтрона и ядра. Так как в справочных таблицах приводятся массы нейтральных атомов, а не ядер, то дефект массы вычислим по формуле:
– соответственно масса протона, нейтрона и ядра. Так как в справочных таблицах приводятся массы нейтральных атомов, а не ядер, то дефект массы вычислим по формуле:
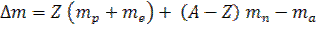 . (2)
. (2)
Так как 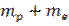 =
= 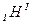 , где m
, где m 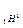 - масса изотопа водорода
- масса изотопа водорода 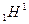 , то формула (2) примет вид:
, то формула (2) примет вид: 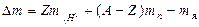 (3)
(3)
Подставим в выражение (3) числовые данные и вычислим
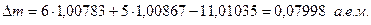
В соответствии с законом взаимосвязи массы и энергии, Дж
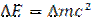 , (4)
, (4)
где 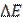 - энергия связи, численно равная работе, которую необходимо затратить, чтобы разделить ядро на отдельные, не взаимодействующие между собой частицы без сообщения им кинетической энергии;
- энергия связи, численно равная работе, которую необходимо затратить, чтобы разделить ядро на отдельные, не взаимодействующие между собой частицы без сообщения им кинетической энергии; 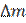 - дефект массы ядра; с – скорость света в вакууме.
- дефект массы ядра; с – скорость света в вакууме.
Так как дефект массы выражен во внесистемных единицах (а.е.м.), то энергия связи ядра: 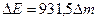 МэВ(5)
МэВ(5)
Подставим в формулу (5) числовое значение дефекта массы и вычислим 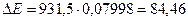 (МэВ).
(МэВ).
Ответ: 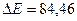 МэВ
МэВ
Пример№ 4. Найти удельную энергию связи нуклонов в ядрах 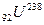 и
и 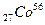 . Ядро какого элемента наиболее устойчиво?
. Ядро какого элемента наиболее устойчиво?
Дано:
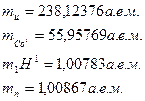 | Решение: Удельная энергия связи нуклонов в ядре – это энергия связи, приходящаяся на один нуклон. Удельная энергия связи может быть вычислена по формуле 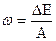 , (1) , (1) |
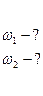 | где 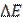 – энергия связи нуклонов в ядре, равная – энергия связи нуклонов в ядре, равная 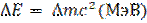 ; A- массовое число, указывающее на число нуклонов в ядре; ; A- массовое число, указывающее на число нуклонов в ядре; 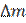 - дефект массы нуклонов в ядре; с2 =931,5 Мэв/а.е.м. – скорость света в вакууме во внесистемных единицах. - дефект массы нуклонов в ядре; с2 =931,5 Мэв/а.е.м. – скорость света в вакууме во внесистемных единицах. |
Если дефект массы выразить в атомных единицах массы, то энергия связи нуклонов в ядре может быть вычислена по формуле, МэВ
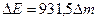 МэВ. (2)
МэВ. (2)
Дефект массы ядра определяется разностью масс свободных нуклонов и массой ядра: 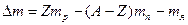 (3), где Z – число протонов в ядре – порядковый номер элемента; (А-Z) – число нейтронов в ядре;
(3), где Z – число протонов в ядре – порядковый номер элемента; (А-Z) – число нейтронов в ядре; 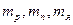 – соответственная масса протона, нейтрона и ядра элемента. В справочных таблицах приводятся массы не ядер, а нейтральных атомов, поэтому преобразуем формулу (3) так, чтобы пользоваться массой нейтрального атома
– соответственная масса протона, нейтрона и ядра элемента. В справочных таблицах приводятся массы не ядер, а нейтральных атомов, поэтому преобразуем формулу (3) так, чтобы пользоваться массой нейтрального атома
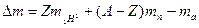 (4), где
(4), где 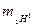 - масса изотопа атома водорода.
- масса изотопа атома водорода.
Подставим формулу (4) в (2) и полученное выражение 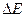 в формулу (1), получим формулу для расчета удельной энергии связи
в формулу (1), получим формулу для расчета удельной энергии связи
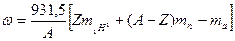 . (5)
. (5)
Подставим числовые данные и вычислим удельную энергию связи:
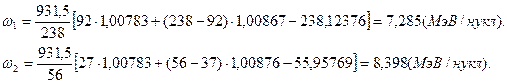
Так как удельная энергия связи нуклонов в ядре кобальта больше удельной энергии связи ядра урана, то более устойчиво ядро кобальта.
Ответ: 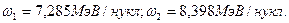 Устойчивее ядро кобальта.
Устойчивее ядро кобальта.
Пример № 5. Вычислить в мегаэлектроновольтах энергию ядерной реакции
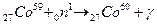 . Выделяется или поглощается энергия при этой реакции?
. Выделяется или поглощается энергия при этой реакции?
Дано:
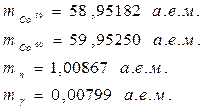 | Решение: Чтобы вычислить энергию ядерной реакции 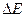 необходимо знать дефект массы реакции необходимо знать дефект массы реакции 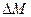 , так как , так как 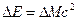 , где с – скорость света. Если , где с – скорость света. Если 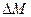 выражать в а.е.м., формула примет вид: выражать в а.е.м., формула примет вид: |
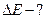 | 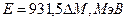 . (1) . (1) |
 Дефект массы:
Дефект массы: 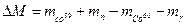 . (2)
. (2)
Так как число электронов до и после реакции сохраняется, вместо значений масс ядер воспользуемся значениями масс нейтральных атомов:
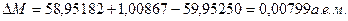
Реакция протекает с выделением энергии, так как 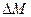 >0. Подставив значение
>0. Подставив значение 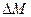 в (1), получим
в (1), получим
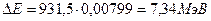 . Реакция экзотермическая.
. Реакция экзотермическая.
Ответ: 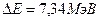 . Реакция экзотермическая.
. Реакция экзотермическая.
3.3. Базовые задачи для самостоятельного решения
1. Определить энергию фотона, соответствующего второй линии в первой инфракрасной серии Пашена спектра атома водорода.
Ответ: 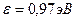
2. Найти энергию ионизации атома водорода(минимальную энергию, необходимую чтобы оторвать электрон от атома)
Ответ: 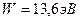
3. Найти отношение длин волн вторых по порядку спектральных линий серии Бальмера и Пашена.
Ответ: 2,64
4. Вычислить для иона 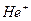 радиус первой боровской орбиты и скорость электрона на ней
радиус первой боровской орбиты и скорость электрона на ней
Ответ: Z=26,5 пм; 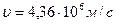
5. Вычислить с помощью закона Мозли длину волны 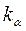 - линии алюминия и кобальта. (Постоянную экранирования для К-серии считать равной единице).
- линии алюминия и кобальта. (Постоянную экранирования для К-серии считать равной единице).
Ответ: 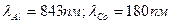
6. Определить коротковолновую границу сплошного спектра рентгеновского излучения, если рентгеновская трубка работает под напряжением 30 кВ
Ответ: 41пм
7. При каком наименьшем напряжении на рентгеновской трубке начинают появляться линии К-серии меди?
Ответ: 8кВ
8. Вычислить дефект массы и энергию связи ядра 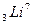 .
.
Ответ: 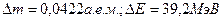
9. При соударении 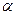 -частицы с ядром бора
-частицы с ядром бора 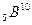 произошла ядерная реакция, в результате которой образовалось 2 новых ядра. Одним из этих ядер было ядро атома водорода
произошла ядерная реакция, в результате которой образовалось 2 новых ядра. Одним из этих ядер было ядро атома водорода 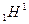 . Определить порядковый номер и массовое число второго ядра, определить энергетический эффект протекающей ядерной реакции.
. Определить порядковый номер и массовое число второго ядра, определить энергетический эффект протекающей ядерной реакции.
Ответ: 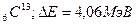
10. Дописать ядерную реакцию и вычислить ее тепловой эффект: 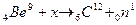 .
.
Ответ: 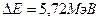
11. Вычислить энергию ядерной реакции 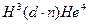 .
.
Ответ: 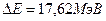
12. Какой изотоп образуется из 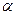 -активного
-активного 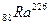 в результате 5
в результате 5 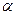 -распадов и трех
-распадов и трех 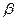 -распадов?
-распадов?
Ответ: 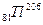
13. Определить порядковый номер и массовое число частицы, обозначенной буквой х, в символической записи ядерной реакции 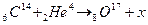
Ответ: А=1; Z=0; частица – нейтрон.
14. Сравнить отношение длин волн де Бройля для электрона и шарика массой m=1г, движущихся с одинаковой скоростью.
Ответ: 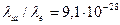
15. Найти длину волны де Бройля для электрона, кинетическая энергия которого равна 1МэВ.
Ответ: 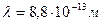
16. Вычислить длину волны де Бройля для электрона, протона и атома урана, имеющих одинаковую кинетическую энергию 100эВ.
Ответ: 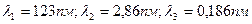
17. Определить число атомов радиоактивного препарата йода 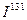 , массой 0,5мкг, распавшихся в течение 1 мин, 1 недели.
, массой 0,5мкг, распавшихся в течение 1 мин, 1 недели.
Ответ: 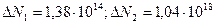
18. Период полураспада радия 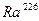 составляет 1620 лет. Найти постоянную распада.
составляет 1620 лет. Найти постоянную распада.
Ответ: 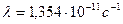
19. Из каждого миллиона атомов радиоактивного изотопа каждую секунду распадается 200 атомов. Определить период полураспада.
Ответ: 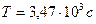
20. Определить дефект массы и энергию связи ядра атома тяжелого водорода 1Н3.
Ответ: 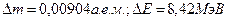
3.4. Контрольные вопросы
 2015-03-08
2015-03-08 1936
1936
