Вероятность возникновения внешнего фотоэффекта в металле намного выше, чем в других веществах, так как в нем есть сводные электроны, которые и могут покинуть его.
Облучение полупроводников потоком фотонов приводит к увеличению их проводимости и этот эффект называется внутренним фотоэффектом.
В 1888-1889 годах профессор Петербургского университета Александр Столетов на основании своих экспериментальных исследований внешнего фотоэффекта сформулировал три закона:
1. Сила тока насыщения (максимальный ток между катодом и анодом) в фотодиоде пропорциональна мощности падающего светового потока и не зависит от частоты падающего излучения.
Чем больше мощность светового потока, тем больше фотонов падает на поверхность металла, тем большее их количество поглощается электронами, которые, совершив работу выхода, вырываются из металла.
2. Максимальная скорость фотоэлектронов зависит только от частоты падающего излучения и не зависит от его мощности.
При поглощении фотона электрон приобретает энергию 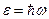 , которую тратит на совершение работы против сил притяжения кристаллической решетки и на создание начального запаса кинетической энергии.
, которую тратит на совершение работы против сил притяжения кристаллической решетки и на создание начального запаса кинетической энергии.
|
|
|
Величина этой работы определяется свойствами кристаллической решетки, и минимальное ее значение называется работой выхода (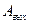 ).
).
3. Существует минимальная частота (или максимальная длина волны) электромагнитного излучения, при которой еще возможен фотоэффект.
Эту частоту называют красной границей фотоэффекта.
Если энергии поглощенного фотона хватает только на совершение работы выхода, то начальная скорость вылетевших электронов практически равна нулю.
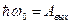
В 1905 году Эйнштейн, опираясь на закон сохранения энергии и предположив, что вещество не только излучает энергию порциями, но и поглощает его тоже порциями, вывел уравнение, которое называют уравнением Эйнштейна для фотоэффекта:
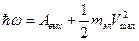
По Эйнштейну, дополнительную энергию электрон получит, поглотив фотон с энергией 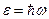 , которая усваивается им целиком. Часть этой энергии электрон затрачивает на совершение работы против сил взаимодействия с кристаллической решеткой, чтобы покинуть катод, остаток энергии образует начальный запас кинетической энергии. Если электрон поглощает фотон не у самой поверхности, а на некоторой глубине, то вероятность покинуть тело катода уменьшается, так как большая часть поглощенной энергии теряется при случайных столкновениях в веществе.
, которая усваивается им целиком. Часть этой энергии электрон затрачивает на совершение работы против сил взаимодействия с кристаллической решеткой, чтобы покинуть катод, остаток энергии образует начальный запас кинетической энергии. Если электрон поглощает фотон не у самой поверхности, а на некоторой глубине, то вероятность покинуть тело катода уменьшается, так как большая часть поглощенной энергии теряется при случайных столкновениях в веществе.
Фотоэффект невозможно объяснить с помощью классической волновой теории света, что служило подтверждением гипотезы Планка о квантовой природе электромагнитного излучения.
В 1889 году Эдуард Ленард и Дж. Дж. Томсон, усовершенствовав прибор Столетова,
|
|
|
Рис5, получили вольтамперную характеристику первого фотодиода Рис 6.
Рис.5 Рис 6
Схема вакуумного фотодиода Вольтамперная характеристика вакуумного
фотодиода
Как видно из графика, при постоянстве падающего светового потока и при нулевой разности потенциалов U между катодом (К) и анодом (А) фототок I не равен нулю. Это объясняется тем, что, поглотив фотон и совершив работу выхода 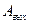 , самые быстрые электроны при удачном направлении вектора начальной скорости могут долететь до анода. Поле между катодом и анодом ускоряет вылетевшие электроны и, чем оно сильнее, тем большее их количество попадает на анод. При некотором напряжении рост фототока прекращается, так как все вылетевшие в единицу времени электроны попали на анод (
, самые быстрые электроны при удачном направлении вектора начальной скорости могут долететь до анода. Поле между катодом и анодом ускоряет вылетевшие электроны и, чем оно сильнее, тем большее их количество попадает на анод. При некотором напряжении рост фототока прекращается, так как все вылетевшие в единицу времени электроны попали на анод (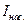 ).
).
Чем больше мощность светового потока, тем больше фотонов падает на поверхность катода, тем больше электронов вырывается из нее, тем больше ток насыщения 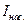 .
.
(первый закон Столетова).
Чем больше частота падающих фотонов, тем больше энергии поглощает электрон, и тем больше ее остается у него после совершения работы выхода в виде кинетической энергии
(2-ой закон Столетова).
Для полного прекращения фототока необходимо приложить обратное напряжение между катодом и анодом (к катоду плюс, а к аноду минус). Обратное напряжение, при котором даже самым быстрым электронам не удается долететь до анода, называется задерживающей разностью потенциалов. При этом вылетевший электрон тратит всю свою кинетическую энергию на преодоления тормозящего действия внешнего поля, поэтому можно записать, что:
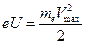 .
.
Непосредственное подтверждение гипотезе Эйнштейна о дискретности процессов излучения и поглощения энергии веществом дал в 1924 году опыт Боте.
Схема опыта приведена на рис 7.
Рис.7
Схема опыта Боте.
Тонкая металлическая фольга (1) помещалась между двумя газоразрядными счетчиками (2). Фольга освещалась слабым потоком рентгеновских лучей, что приводило к вторичному рентгеновскому излучению (рентгеновская флуоресценция), мощность которого тоже была невелика. Вторичное излучение от фольги попадало в счетчики. Если бы излучаемая энергия была непрерывна и равномерно распределялась по всем направлениям, то счетчики срабатывали бы одновременно. В действительности же наблюдалось беспорядочное их срабатывание. Это можно объяснить только тем, что в отдельных актах испускания возникают световые частицы, летящие в различных направлениях.
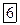 В свое время Максвелл теоретически предсказал существование светового давления на проводящую поверхность, исходя из законов классической электродинамики. В 1901 году русский физик Александр Лебедев экспериментально проверил расчеты Максвелла и измерил световое давление. Кроме того, он показал, что свет оказывает давление на любую поверхность, независимо от ее природы..
В свое время Максвелл теоретически предсказал существование светового давления на проводящую поверхность, исходя из законов классической электродинамики. В 1901 году русский физик Александр Лебедев экспериментально проверил расчеты Максвелла и измерил световое давление. Кроме того, он показал, что свет оказывает давление на любую поверхность, независимо от ее природы..
В общем случае существование светового давления можно объяснить, только считая свет потоком фотонов.
Пусть на единицу поверхности в единицу времени падает энергия, равная Е, которую приносят N фотонов, тогда
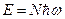 .
.
Каждый фотон передает ей импульс, равный:
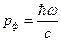
По определению давление есть импульс, переданный единице поверхности в единицу времени.
Если поверхность идеально поглощающая, то полученный ее импульс равен
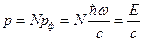 .
.
Если поверхность идеально отражающая, то полученный ее импульс равен:
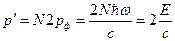 .
.
Если поверхность имеет коэффициент отражения равный R, то из N фотонов, падающих на единицу поверхности в единицу времени, поглотится 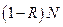 фотонов и отразится
фотонов и отразится 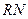 фотонов. Следовательно, общий импульс, полученный единицей поверхности, будет равен:
фотонов. Следовательно, общий импульс, полученный единицей поверхности, будет равен:
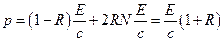
где р- давление света в паскалях, 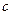 - скорость света в вакууме,
- скорость света в вакууме, 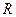 - коэффициент отражения от данной поверхности,
- коэффициент отражения от данной поверхности, 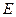 - полная энергия светового потока, падающая на единицу площади в единицу времени.
- полная энергия светового потока, падающая на единицу площади в единицу времени.
|
|
|
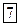 Рентгеновские лучи возникают при бомбардировке поверхности твердых тел быстрыми электронами. Они были открыты в 1885 году немецким физиком Рентгеном.
Рентгеновские лучи возникают при бомбардировке поверхности твердых тел быстрыми электронами. Они были открыты в 1885 году немецким физиком Рентгеном.
Схема рентгеновской трубки представлена на Рис 8.
Рис.8
Нагреваемый током катод К служит источником свободных электронов, которые вылетают из него вследствие термоэлектронной эмиссии. Мишенью является анод А, который называют антикатодом. Ускоренные высоким напряжением между катодом и антикатодом электроны, попав в вещество антикатода, испытывают сильное торможение и становятся источниками электромагнитного излучения.
Спектр этого излучения имеет вид представленный на Рис.9
Рис.9
Часть излучения, которая имеет непрерывный спектр и описывается «гладкой» функцией 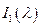 , испускается самими электронами при торможении. Эту часть излучения и называют тормозным.
, испускается самими электронами при торможении. Эту часть излучения и называют тормозным.
Как видно из графика в спектре отсутствуют волны, длина которых меньше некоторого значения  . Наличие коротковолновой границы объясняется тем, что тормозящий электрон не может излучить энергии больше своего запаса кинетической энергии. Причем, значение
. Наличие коротковолновой границы объясняется тем, что тормозящий электрон не может излучить энергии больше своего запаса кинетической энергии. Причем, значение  зависит от ускоряющего напряжения между катодом и мишенью и не зависит от материала мишени:
зависит от ускоряющего напряжения между катодом и мишенью и не зависит от материала мишени:
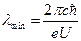 ,
,
где с- скорость света в вакууме, е- заряд электрона, 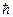 - приведенная постоянная Планка, U- напряжение между катодом и мишенью.
- приведенная постоянная Планка, U- напряжение между катодом и мишенью.
Функция 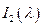 - представляет собой последовательность острых пиков. Вид этой функции определяется свойствами вещества мишени. Это излучение дают сами атомы, которые, получив от электронов при столкновении дополнительную энергию, переходят в возбужденное состояние, а затем, возвращаясь в основное состояние, излучают ее в виде квантов высокой частоты. Это излучение называют характеристическим.
- представляет собой последовательность острых пиков. Вид этой функции определяется свойствами вещества мишени. Это излучение дают сами атомы, которые, получив от электронов при столкновении дополнительную энергию, переходят в возбужденное состояние, а затем, возвращаясь в основное состояние, излучают ее в виде квантов высокой частоты. Это излучение называют характеристическим.
 В 1923 году американский физик Артур Холли Комптон, исследуя спектральный состав рентгеновских лучей, прошедших через легкие вещества (графит, парафин), обнаружил, что в рассеянном излучении присутствуют волны, длина которых больше, чем у падающих волн, т.е
В 1923 году американский физик Артур Холли Комптон, исследуя спектральный состав рентгеновских лучей, прошедших через легкие вещества (графит, парафин), обнаружил, что в рассеянном излучении присутствуют волны, длина которых больше, чем у падающих волн, т.е 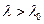 . Схема опыта Комптона приведена на рис.10. Выделяемый двумя диафрагмами (Д) узкий пучок монохроматического рентгеновского излучения направлялся на рассеивающее вещество (РВ). Спектральный состав рассеянного излучения исследовался с помощью рентгеновского спектрографа, состоящего из кристалла (Кр) и ионизационной камеры (ИК).
. Схема опыта Комптона приведена на рис.10. Выделяемый двумя диафрагмами (Д) узкий пучок монохроматического рентгеновского излучения направлялся на рассеивающее вещество (РВ). Спектральный состав рассеянного излучения исследовался с помощью рентгеновского спектрографа, состоящего из кристалла (Кр) и ионизационной камеры (ИК).
|
|
|
Рис.10 Схема опыта Комптона.
Было установлено, что комптоновское излучение подчиняется следующим закономерностям:
1. Наиболее интенсивное комптоновское излучение наблюдается при рассеянии на атомах легких элементов;
2. При увеличении угла рассеивания интенсивность комптоновского излучения возрастает, в то время как у классического излучения наоборот падает;
3. Смещение длины волны комптоновского излучения 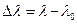 зависит от угла
зависит от угла  между направлениями первичного и рассеянного излучения и не зависит от длины волны падающего излучения, ни от природы рассеивающего вещества.
между направлениями первичного и рассеянного излучения и не зависит от длины волны падающего излучения, ни от природы рассеивающего вещества.
4. При одинаковых углах рассеивания 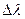 одинакова для любых веществ и равна:
одинакова для любых веществ и равна:
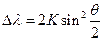 ,
,
где К- константа Комптона,  - угол рассеивания.
- угол рассеивания.
Изменение длины волны рассеянных фотонов обусловлено взаимодействием падающих фотонов с внешними электронами, которые слабо связаны со своими атомами и могут быть почти свободными и их можно считать покоящимися.
Пусть падающий фотон обладает энергией 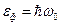 и импульсом
и импульсом 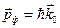 , энергия электрона до столкновения с фотоном, по Эйнштейну, равна
, энергия электрона до столкновения с фотоном, по Эйнштейну, равна 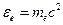 и его импульс равен
и его импульс равен 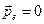 . После столкновения электрон приобретает импульс
. После столкновения электрон приобретает импульс 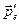 и энергию равную
и энергию равную 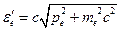 . Рассеянный фотон после столкновения имеет энергию равную
. Рассеянный фотон после столкновения имеет энергию равную 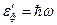 и импульс
и импульс  .
.
Рис.11
Рассеяние рентгеновского фотона на первоначально покоящемся электроне.
Из законов сохранения энергии и импульса получим два уравнения:
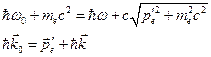
Разделив первое уравнение на с (скорость света в вакууме), перегруппировав в нем слагаемые и возведя левую и правую части его в квадрат и учитывая, что  , получим:
, получим:
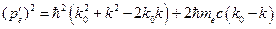
Возведем в квадрат второе уравнение и раскрывая скалярное произведение двух векторов, получим:
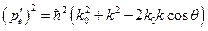 ,
,
где  - угол между векторами
- угол между векторами 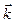 и
и 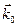 .
.
Приравняв первое и второе полученные выражения, получим:
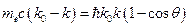 .
.
Учитывая, что 
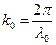 , и умножив левую и правую части полученного уравнения на
, и умножив левую и правую части полученного уравнения на 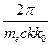 , получим:
, получим:
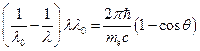 .
.
Обозначим 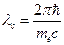 . Эту константу называют комптоновской длиной волны электрона и она равна
. Эту константу называют комптоновской длиной волны электрона и она равна 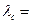 2,43
2,43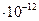 м.
м.
В результате: 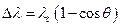 .
.
При рассеянии фотонов на электронах, имеющих сильную связь со своим атомом, обмен энергией и импульсом происходит с атомом в целом. Поскольку масса атома много больше массы электрона комптоновское смещение будет ничтожным. Поэтому с ростом атомного номера рассеивающего вещества в таблице Менделеева эффект Комптона становится слабее выражен.
Мы с Вами разобрали явления, которые свидетельствовали как в пользу волновой теории
(интерференция, дифракция, поляризация и дисперсия), так и в пользу корпускулярной теории (фотоэффект, эффект Комптона, тормозное излучение и световое давление). Так свет волна или частица? Нильс Бор в своем принципе дополнительности сформулировал ответ на этот вопрос так: для объяснения конкретного эксперимента надо использовать либо волновые, либо корпускулярные представления о свете, но никогда те и другие одновременно. Для полного понимания природы света необходимо учитывать оба представления.
По современным представлениям свет обладает корпускулярно-волновым дуализмом.
ЛЕКЦИЯ 3.
ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
1. Гипотеза де Бройля.
2. Соотношение неопределенности Гайзенберга.
3.Волновая функция и ее интерпретации.
4. Уравнение Шредингера. Стационарные состояния.
 В 1924 году французский физик Луи де Бройль выдвинул гипотезу о том, что дуализм не является особенностью фотона и что подобным свойством обладает любая материя.
В 1924 году французский физик Луи де Бройль выдвинул гипотезу о том, что дуализм не является особенностью фотона и что подобным свойством обладает любая материя.
Он писал: «в оптике в течение столетия слишком пренебрегали корпускулярным способом рассмотрения процессов по сравнению с волновым, не делается ли в теории вещества обратная ошибка».
По де Бройлю: всякий микрообъект, будь то молекула, атом, электрон или фотон, представляет собой образование особого рода, сочетающее в себе свойства и волны и частицы; при этом микротела не ведут себя ни как частица, ни как волна.
Допуская, что микрочастицы наряду с корпускулярными обладают и волновыми свойствами, он перенес на случай частиц вещества те же правила перехода от одной картины к другой, какие справедливы в случае света.
Мы знаем, что фотон обладает энергией  и импульсом
и импульсом 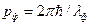 .
.
Де Бройль считал, что движение релятивистской микрочастицы связано с волновым процессом, длина волны которого определяется ее импульсом и энергией.
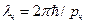 ,
, 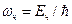 .
.
Для нерелятивистской частицы, скорость которой меньше скорости света длина волны вещества может быть определена по формуле:
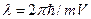 .
.
Гипотеза де Бройля была подтверждена уже в 1927году американскими физиками Дэвиссоном и Джермером, которые получили дифракцию электронов, используя в качестве отражающей дифракционной решетки монокристалл никеля. В том же 1927 году англичанин Дж. Томсон (сын известного физика Дж.Дж Томсона, которому принадлежит первая модель атома) и советский физик П. Тартаковский получили дифракционную картину при прохождении электронного пучка через металлическую фольгу. Полученные результаты практически идеально совпадали с результатами, вычисленными по формуле Брегов для дифракции рентгеновских лучей.
Микрообъект не способен воздействовать непосредственно на наши органы чувств – ни видеть, ни осязать его нельзя. Ничего подобного микрообъектам в воспринимаемом нами мире не существует. Мы знаем, что будет с макрочастицей, можем предсказать траекторию ее движения, но микрочастицы так себя не ведут.
Отличие микрочастицы от привычных нам макротел в том, что она не обладает одновременно определенными значениями координаты и импульса. Вследствие чего привычное понятие «траектория движение» утрачивает смысл.
Своеобразие свойств микрочастиц отчетливее всего обнаруживается в следующем мысленном эксперименте. Направим на преграду с двумя узкими щелями параллельный
пучок монохроматических (обладающих одинаковой кинетической энергией) электронов, рис.12.
Рис. 12
Дифракция электронного пучка на двух щелях.
За преградой поставим фотопластинку. Сначала пропустим пучок через одну щель, потом через другую. На пластинке возникнут почернения в виде кривых 1 и 2. Затем откроем обе щели и пропустим пучок через них. Возникшая картина не является наложением двух предыдущих, что свидетельствует о влиянии обоих отверстий на движение каждого электрона. Такой вывод не совместим с представлением о траекториях. Если бы электрон находился в каждый момент времени в определенной точке пространства, то он проходил бы только через одно отверстие. Явление же дифракции доказывает, что в прохождении каждого электрона участвуют оба отверстия. Это не означает, что через каждое отверстие проходит часть электрона, так как электрон, как и любая микрочастица, является неделимым целым.
Проведенный эксперимент доказывает, что микрочастицы обладают свойствами особого рода, совершенно отличными от свойств макрочастиц.
Из сказанного следует, что монохроматический поток микрочастиц, каждая из которых обладает импульсом 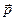 и энергией Е, при определенных условиях будет вести себя как плоская монохроматическая волна с волновым числом
и энергией Е, при определенных условиях будет вести себя как плоская монохроматическая волна с волновым числом 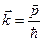 и частотой
и частотой 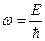 .
.
Эту волну можно описать комплексной функцией вида:
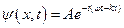 или
или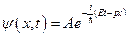 , где i- мнимая единица.
, где i- мнимая единица.
 В классической механике состояние макрочастицы определяются заданием значений координат, импульса, энергии и т.д. Эти величины называются динамическими переменными.
В классической механике состояние макрочастицы определяются заданием значений координат, импульса, энергии и т.д. Эти величины называются динамическими переменными.
Как уже говорилось, своеобразие свойств микрочастиц проявляются в том, что для определения ее состояния не для всех переменных, которые должны определять это состояние, могут быть получены конкретные значения.
В 1927 году немецкий физик Гайзенберг математически доказал, что: произведение неопределенностей значений двух канонически сопряженных переменных не может быть по порядку величины меньше постоянной Планка.
Это утверждение называется принципом неопределенности Гайзенберга.
В механике канонически сопряженными являются пары переменных: координата (x,y,z) и импульс (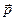 ); энергия Е и время t.
); энергия Е и время t.
Математически принцип неопределенности можно записать:
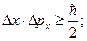
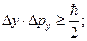
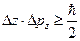
или 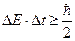 .
.
Рассмотрим микрочастицу свободно летящую вдоль оси ОY. Поставим на ее пути преграду со щелью шириной 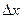 , расположенную перпендикулярно направлению ее движения, рис. 13.
, расположенную перпендикулярно направлению ее движения, рис. 13.
Рис.13
Дифракция частицы на одной щели.
До прохождения щели х-ая компонента импульса частицы имеет точное значение 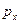 =0, так как ось ОХ направлена перпендикулярно ее движению, следовательно, неопределенность импульса тоже равна нулю
=0, так как ось ОХ направлена перпендикулярно ее движению, следовательно, неопределенность импульса тоже равна нулю 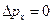 . Координата же частицы в этот момент является совершенно неопределенной. После прохождения щели появляется неопределенность координаты равная
. Координата же частицы в этот момент является совершенно неопределенной. После прохождения щели появляется неопределенность координаты равная 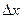 , но достигается это потерей определенности импульса, так как вследствие дифракции имеется некоторая вероятность того, что частица будет двигаться в пределах угла равного
, но достигается это потерей определенности импульса, так как вследствие дифракции имеется некоторая вероятность того, что частица будет двигаться в пределах угла равного 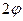 . Угол
. Угол 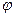 соответствует положению первого дифракционного максимума. Максимумами высших порядков можно пренебречь, поскольку их интенсивность будет мала по сравнению с интенсивностью центрального максимума.
соответствует положению первого дифракционного максимума. Максимумами высших порядков можно пренебречь, поскольку их интенсивность будет мала по сравнению с интенсивностью центрального максимума.
Таким образом, неопределенность импульса будет равна:
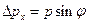 .
.
Из теории дифракции известно, что краю центрального дифракционного максимума (это первый дифракционный минимум) соответствует угол, синус которого равен:
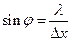 .
.
Подставив синус в неопределенность импульса получим величину, оговоренную в принципе неопределенности Гайзенберга:
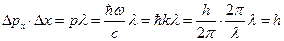 .
.
Соотношение неопределенностей обусловлено корпускулярно-волновым дуализмом микрочастиц. Оно указывает, в какой мере можно пользоваться понятиями классической механики применительно к объектам микромира, которые подчиняются более тонким закономерностям, основанным на вероятностном подходе.
 Итак, согласно гипотезе де Бройля, любая материя обладает корпускулярно- волновым дуализмом. Следовательно, для полного описания состояния микрочастицы надо использовать как стандартные характеристики корпускул (массу, импульс), так и волновые. Одной из основных характеристик, описывающих волну, является ее амплитуда. Каков же физический смысл амплитуды волны де Бройля (волны материи)?
Итак, согласно гипотезе де Бройля, любая материя обладает корпускулярно- волновым дуализмом. Следовательно, для полного описания состояния микрочастицы надо использовать как стандартные характеристики корпускул (массу, импульс), так и волновые. Одной из основных характеристик, описывающих волну, является ее амплитуда. Каков же физический смысл амплитуды волны де Бройля (волны материи)?
В квантовой механике амплитуду волны материи задают волновой функцией 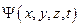 (пси ).
(пси ).
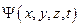 - это заданная в любой точке пространства и в любой момент времени амплитуда волны материи, подобно тому, как вектор
- это заданная в любой точке пространства и в любой момент времени амплитуда волны материи, подобно тому, как вектор 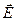 есть амплитуда электромагнитной волны.
есть амплитуда электромагнитной волны.
Что бы понять физический смысл волновой функции, описывающей поток частиц, воспользуемся аналогией со светом.
По определению, интенсивность электромагнитной волны пропорциональна квадрату ее амплитуды: 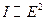 . С другой стороны, интенсивность светового пучка пропорциональна числу фотонов, падающих на единицу поверхности в единицу времени:
. С другой стороны, интенсивность светового пучка пропорциональна числу фотонов, падающих на единицу поверхности в единицу времени: 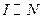 .
.
Следовательно, 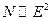 .
.
Таким образом, если волновая функция 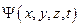 описывает ансамбль, состоящий из большого количества частиц, то
описывает ансамбль, состоящий из большого количества частиц, то 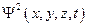 в любой точке пространства пропорциональна числу частиц, которые могут быть обнаружены в данной точке в данный момент времени.
в любой точке пространства пропорциональна числу частиц, которые могут быть обнаружены в данной точке в данный момент времени.
Физический смысл волновой функции, описывающей поведение одной частицы, дал в 1926 г. Макс Борн.
Согласно Борну, квадрат модуля волновой функции определяет вероятность dW того, что частица будет обнаружена в пределах объема dV:
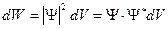
Интеграл от этого выражения, взятый по всему объему должен быть равен единице, так как он дает вероятность того, что частица находится в одной из точек объемаV, а вероятность достоверного события всегда равна единице.
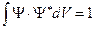
 2014-02-02
2014-02-02 1651
1651
