Решение. Величина бесконечно возрастает с ростом n

Величина бесконечно возрастает с ростом n. Поэтому предел последовательности S_n при n ® ¥ равен бесконечности и ряд расходится.

Пример. Определить сходимость следующего ряда:

1 - 1 + 1 - 1 + (-1)ⁿ⁺¹ +....

Решение. Четная частичная сумма этого ряда S_2n = 0, а нечетная - S_2n+1 = 1. Это означает, что предел не существует. Следовательно, данный ряд расходится.

Необходимое условие сходимости ряда. Для сходящихся числовых рядов всегда выполняется одно условие - его общий член стремится к нулю. Дадим строгую формулировку необходимого условия сходимости ряда.

Теорема о необходимом условии сходимости числового ряда. Если числовой ряд сходится, то его общий член при n ® ¥ стремится к нулю, т.е.

(1.4)

Доказательство. Рассмотрим две соседние частичные суммы ряда (1.2)

S_n-1 = u₁ + u₂ + u₃ +... u_n-1,

S_n = u₁ + u₂ + u₃ +... u_n-1 + u_n.

Из сходимости ряда следует, что

С другой стороны,

т.е.

S = S +

откуда и следует (4).

Введенное условие сходимости является лишь необходимым, но не достаточным. Это означает, что существуют расходящиеся ряды, у которых.

Пример. Покажем, что ряд

удовлетворяет необходимому условию сходимости ряда, но является расходящимся.

Действительно, необходимое условие выполняется, так как

Чтобы доказать расходимость ряда, рассмотрим его n-ю частичную сумму:

Очевидно, что ряд расходится, поскольку

Основные свойства сходящихся числовых рядов.

Свойство 1. Добавление или отбрасывание конечного числа членов не изменяет сходимости ряда.

Доказательство. Пусть A - сумма отброшенных (добавленных) членов ряда, а S_n - частичная сумма исходного ряда (2). Тогда частичная сумма ряда с отброшенными (добавленными) членами имеет вид S^* = S_n ± A.

Поскольку A - конечное число, то

Следовательно, если существует то существует и

Свойство 2. Если ряд

u₁ + u₂ + u₃ +.... + u_n +... (1.5)

сходится и имеет сумму S, то ряд cu₁ + cu₂ +... + cu_n +.., получаемый из предыдущего умножением всех членов на одно и то же число с, также сходится и имеет сумму с∙S.

Доказательство. Рассмотрим частичную сумму ряда (1.5):

s_n = cu₁ + cu₂ + cu₃ +... + cu_n = c∙S_n.

Поэтому

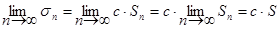
Свойство 3. Сходящиеся ряды можно почленно складывать и вычитать.

Доказательство. Пусть

u₁ + u₂ + u₃ +... + u_n +... = S;

v₁ + v₂ + v₃ +... + v_n +... = Ф,

тогда ряд

(u₁ ± v₁) + (u₂ ± v₂) +... + (u_n ± v_n) +...

также сходится и имеет сумму S ± Ф, так как