Глава 5. Экстремум функции двух переменных

Формула Тейлора для функции двух переменных

Формула Тейлора для функции одной переменной приведена в разделе 4

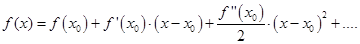
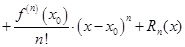
где 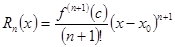остаточный член формулы Тейлора.он определяет погрешность, возникающую при замене функции на полином степени n.

Преобразуем формулу, обозначив за 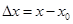и перенесем 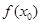налево. Тогда

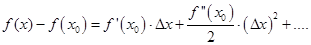
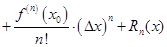
Разность 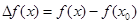есть приращение функции, а 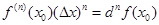. С учетом этих значений, получим дифференциальную форму формулы Тейлора

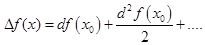
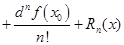(5.1)

Дифференциальная форма справедлива для функции любого числа переменных, в частности, для функции двух переменных,

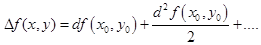
(5.2)

Здесь

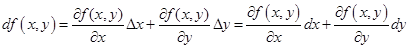
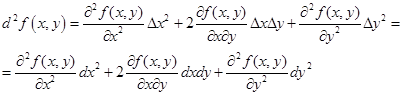
Максимум и минимум функции двух переменных.

Мы говорим, что функция двух переменных z = f (x, у) имеет максимум в точке М₀(x ₀, y ₀), если значение функции в этой точке больше чем во всех соседних точках

f (x ₀, у ₀) > f (x, у)

Аналогично, в точке минимума М₀(x ₀, y ₀) значение функции меньше чем во всех соседних точках

f (x ₀, у ₀) < f (x, у)

минимум и максимум функции достигаются только внутри области D.

Минимумы и максимумы называются экстремумами функции (рис. 4).

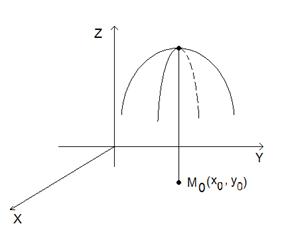
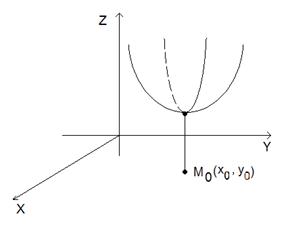
а б

Рис. 4. Максимум (а) и минимум (б) функции двух переменных.

В точке максимума приращение функции отрицательно для любых соседних точек

Δ f (x, y) < 0 (5.3)

В точке минимума приращение всегда строго положительно

Δ f (x, y) > 0 (5.4)

Необходимые условия экстремума. В точке экстремума М₀(x ₀, y ₀) каждая частная производная первого порядка или равна нулю или не существует. Действительно, если мы зафиксируем у = y ₀, то функция f(x, у ₀) будет функцией одной переменной х, а для функции одной переменной в точке экстремума первая производная 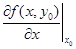или равна нулю или не существует. Аналогично, если х = x ₀, то равна нулю или не существует .

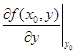Точки, в которых обе частные производные равны нулю называются стационарными точками. Для нахождения стационарной точки необходимо решить систему

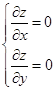(5.5)

Не все стационарные точку будут точками экстремума. Условие (5.5) является только необходимым условием, но не является достаточным.

Достаточные условия экстремума.

Теорема. Если в окрестности стационарной точки М₀(x ₀, y ₀) функция z = f (x, у) имеет непрерывные частные производные до третьего порядка включительно, то функция двух переменных имеет экстремум, если

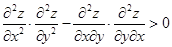(5.6)

При этом

если 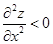, то достигается максимум (5.7)

если 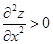, то достигается минимум. (5.8)

Если 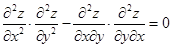, то требуется дальнейшее исследование.

Доказательство. Докажем для максимума, для минимума доказательство аналогично.

В стационарной точке обе частные производные равны нулю, следовательно равен нулю первый дифференциал 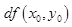и формула Тейлора начинается со второго слагаемого

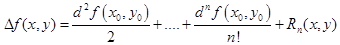
В точке максимума приращение Δ f (x, y) строго отрицательно Δ f (x, y) < 0. Следовательно, необходимо определить, при каких значениях вторых производных второй дифференциал сохраняет знак.

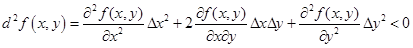
Вынесем за скобки положительную величину 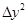=(Δу)², а отношение 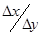обозначим за t 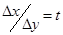. Получим квадратный трехчлен по переменной t, который сохраняет знак при любом значении t только если его дискриминант отрицателен

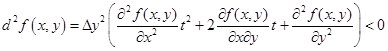
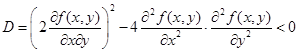
Или, сократив на 4 и переставив члены неравенства, получим

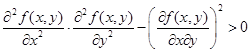
Знак квадратного трехчлена совпадает со знаком коэффициента при t ². Поэтому в точке максимума 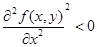. Теорема доказана.

Пример. Исследовать на экстремум функцию .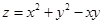

Решение. Вычислим первые производные и найдем стационарную точку

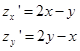
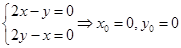
Вычислим вторые производные

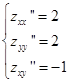
В стационарной точке

z_xx’’∙z_yy’’-(z_xy)²=2∙2-(-1)² > 0,

следовательно это точка экстремума.

Так как z_xx’’ > 0,то это точка минимума.