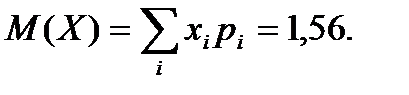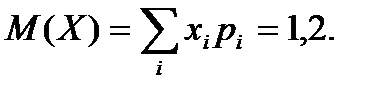Случайная величина Х - это переменная, которая может принимать в зависимости от исходов испытаний те или иные случайные значения хi. Если все значения случайных величин составляют счетное множество, то случайная величина называется дискретной. Ряд количественных показателей экономических систем могут быть рассмотрены как дискретные случайные величины.
Закон распределения случайной дискретной величины связывает между собой значения случайной величины и вероятности принятия случайной величиной ее значений. Он может быть записан в форме таблицы:
| Xi | X0 | X1 | X2 | … | Xk | ИТОГО |
| Pi=P(X=Xi) | P0 | P1 | P2 | … | Pk |
Особое место среди случайных дискретных величин занимают величины с биномиальным законом распределения:
- число наступлений события в независимых повторных испытаниях,
- частота наступлений события в независимых повторных испытаниях.
Характеристики дискретной случайной величины:
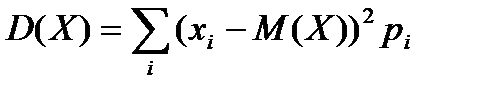 - дисперсия.
- дисперсия.
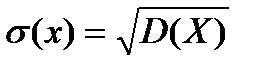 - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
При расчетах дисперсии используют свойство: D(X) = М(Х2)-М2(Х).
Для биномиально распределенных случайных величин можно применять известные формулы расчета характеристик:
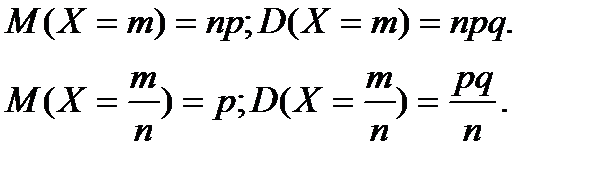
Функция распределения дискретной случайной величины: 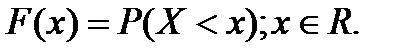
Функция распределения дискретной случайной величины является кусочно-постоянной, она имеет разрывы в точках с координатами, равными значениям случайной величины.
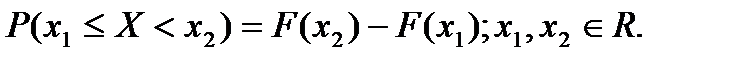
Пример 3.1. У господина "N" имеется три пакета акций различных предприятий. Вероятность получения дохода по пакету акций равна 0,6. Составить закон распределения случайной величины X - числа доходных пакетов акций у господина, определить ее математическое ожидание и дисперсию. Найти вероятность того, что у данного господина не менее двух доходных пакетов акций.
Решение. Для каждого выбранного пакета акций может наступить одно из событий: он не принесет дохода - 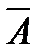 или принесет - А, по условию задачи с вероятностями Р(А)=0,6 = р; Р(
или принесет - А, по условию задачи с вероятностями Р(А)=0,6 = р; Р(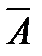 )=0,4 = q. Вероятности событий неизменны для всех пакетов акций, следовательно, имеют место независимые повторные испытания, число которых мало n=3.
)=0,4 = q. Вероятности событий неизменны для всех пакетов акций, следовательно, имеют место независимые повторные испытания, число которых мало n=3.
X – случайная величина, а именно, число доходных пакетов акций у господина. Рассмотрим событие хm=m, состоящее в том, что событие А наступит в n независимых испытаниях m раз. Для определения вероятности данного события следует применять формулу Бернулли. Случайная величина имеет биномиальный закон распределения:
| хm=m | 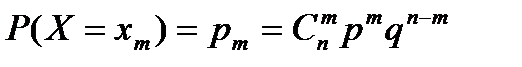 |
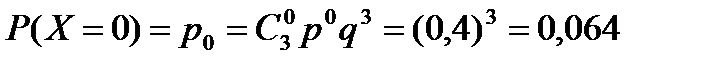 | |
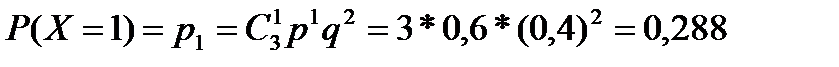 | |
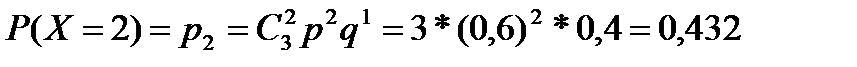 | |
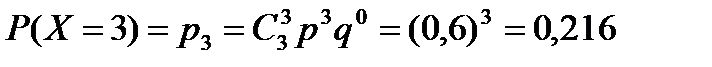 | |
| итого |
Характеристики биномиально распределенной случайной величины можно найти, используя известные формулы:
Математическое ожидание - М(Х=m) =3*0,6=1,8.
Дисперсия – D(X=m) =3*0,6*0,4 = 0,72.
Событие В, состоящее в том, что у господина не менее двух доходных пакетов акций, т.е. или два или три, имеет вероятность:
Р(В) = Р(Х ³ 2) = P(X = 2)+Р(Х = 3) = 0,432 +0,216 = 0,648.
Пример 3.2. В населенном пункте три рынка. Вероятность того, что на рынке есть необходимый для господина N товар, равна 0,6. Он пытается купить этот товар. Если на очередном рынке отсутствует данный товар, господин отправляется за ним на следующий рынок. Поиски прекращаются либо с приобретением товара, либо после того как посещены все рынки. Составить закон распределения числа посещенных рынков. Построить функцию распределения найти математическое ожидание, дисперсию и среднее квадратическое отклонение числа посещенных рынков.
Решение. X - число посещенных рынков. Аi - событие, состоящее в том, что на посещенном рынке есть необходимый товар, 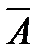 i- товар отсутствует. Вероятности этих событий: P(Аi)=0,6=p; P(
i- товар отсутствует. Вероятности этих событий: P(Аi)=0,6=p; P(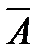 i)=0,4=q; i=1;2;3. Закон распределения и рабочие расчеты по характеристикам случайной величины:
i)=0,4=q; i=1;2;3. Закон распределения и рабочие расчеты по характеристикам случайной величины:
| хi | pi=Р(Х = хi) | XiPi | Xi2Pi |
| pl=P(X=l) = P(Al) = 0,6 | 0,6 | 0,6 | |
p2 = Р(Х = 2)=Р(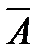 1)*Р(А2)=0,4*0,6 = 0,24 1)*Р(А2)=0,4*0,6 = 0,24 | 0,48 | 0,96 | |
p3 = Р(Х = 3)=Р(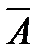 1)*Р( 1)*Р(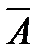 2)=0,4*0,4 = 0,16 2)=0,4*0,4 = 0,16 | 0,48 | 1,44 | |
| å | 1.0 | 1,56 | 3,0 |
Характеристики случайной величины - числа посещенных рынков:
Дисперсия - D(X) = М(Х2)-М2(Х)=3-(1,56)2=0,5664.
Среднее квадратическое отклонение - 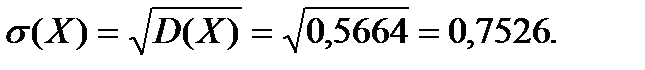
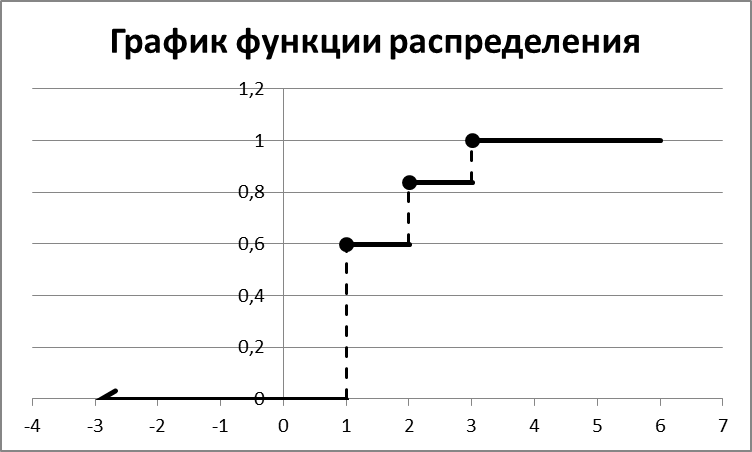
По определению функция распределения случайной величины: F(x)=P(X<x); xÎR.
Следовательно, функция распределения рассматриваемой случайной величины - числа доходных акций господина принимает вид:
| 0; | x£1 | |
| F(X)= | p1=0,6; | 1<х£2 |
| p1+ p2 = 0,6+0,24=0,84; | 2<x£3 | |
| p1+ p2+ p3= 0,6+0,24+0,16 = 1; | х>3 |
Пример 3.3. В урне 10 шаров: 4 белых, остальные – черные. Найти закон распределения случайной величины Х – числа белых шаров, если из урны один за одним не глядя вынули 3 шара. Найти математическое ожидание и дисперсию случайной величины Х. Найти вероятность того, что число вынутых белых шаров окажется больше математического ожидания.
Решение. Х – число белых шаров из 3 взятых. Закон распределения и рабочие расчеты по характеристикам случайной величины:
| хi | pi=Р(Х = хi) | XiPi | Xi2Pi |
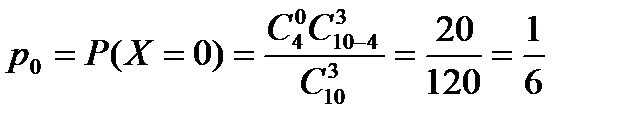 | |||
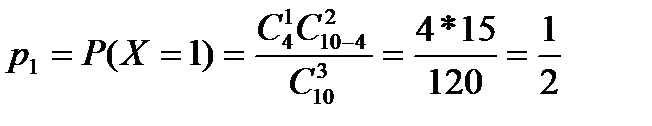 | 0,5 | 0,5 | |
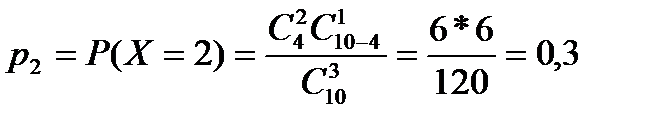 | 0,6 | 1,2 | |
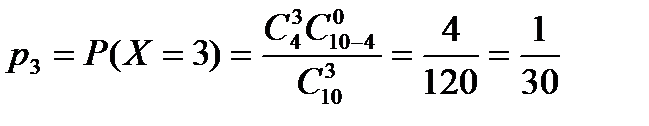 | 0,1 | 0,3 | |
| å | 1.0 | 1,2 | 2,0 |
Характеристики случайной величины Х - числа белых шаров из 3 взятых:
Дисперсия - D(X) = М(Х2)-М2(Х)=2-(1,2)2=0,56.
Вероятность того, что число вынутых белых шаров окажется больше математического ожидания:
P(X>M(X))=P(X>1,2)=P(X=2)+P(X=3)=0,3+1/30=1/3.
Закон распределения дискретной случайной величины Х в данной задаче носит название гипергеометрический закон распределения.
 2015-03-08
2015-03-08 3826
3826

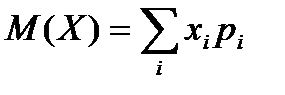 -
-