2015-03-08
283
1. Вычислить теоретические частоты для нормального распределения:
а) выборочное среднее арифметическое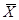 
и выборочное среднее квадратическое отклонение s взять из первой работы;
б) определить вероятности попадания случайной величины в каждый из интервалов по формуле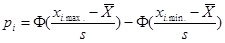 
. Для первого интервала вместо 
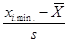взять -∞, для последнего интервала вместо 
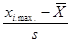взять ∞;
в) определить теоретические частоты ni=n*pi;
г) составить таблицу вида
| [xi min; xi max) | fi | [ ;  )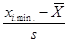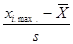
| pi | ni |
д) построить теоретическую кривую распределения.
2. Проверить гипотезу о нормальности по критерию Пирсона:
а) сформулировать нулевую и конкурирующую гипотезы;
б) определить наблюдаемое значение критерия Пирсона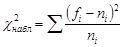 
;
в) определить критическое значение критерия Пирсона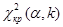 
, где a - уровень значимости, k=m-1-r – число степеней свободы, где m – число разрядов интервального ряда; r – число параметров предполагаемого распределения;
г) сравнить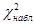 
и 
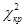; Сделать вывод о необходимости принять (если 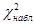< 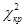), или отвергнуть (если 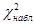> 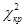) нулевую гипотезу.
3. Проверить гипотезу о нормальности по критерию Колмогорова:
а) составить таблицу накопленных частот
| [xi min; xi max) | mi | pi | Gi=∑mi | Fi=∑pi | |Fi-Gi| |
б) определить значение критерия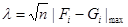 
;
в) по таблице определить P(λ). По значению вероятности сделать вывод о необходимости принять (если P(λ)>0,05), или отвергнуть (если P(λ)<0,05) нулевую гипотезу.
