Закон механики в релятивистской механики

Релятивистская механика — раздел физики, рассматривающий законы механики (законы движения тел и частиц) при скоростях, сравнимых со скоростью света. При скоростях значительно меньших скорости света переходит в классическую (ньютоновскую) механику.

Общие принципы:

В классической механике пространственные координаты и время являются независимыми (при отсутствии голономных связей, зависящих от времени), время является абсолютным, то есть течёт одинаково во всех системах отсчёта, и действуют преобразования Галилея. В релятивистской же механике события происходят в четырёхмерном пространстве, объединяющем физическое трёхмерное пространство и время (пространство Минковского) и действуют преобразования Лоренца. Таким образом, в отличие от классической механики, одновременность событий зависит от выбора системы отсчёта.

Основные законы релятивистской механики — релятивистское обобщение второго закона Ньютона и релятивистский закон сохранения энергии-импульса — являются следствием такого «смешения» пространственных и временной координат при преобразованиях Лоренца.

Второй закон Ньютона в релятивистской механике:

Сила определяется как 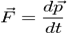также известно выражение для релятивистского импульса: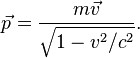

Взяв для определения силы производную по времени от последнего выражения, получим:

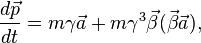где введены обозначения: 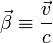и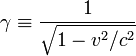

В результате выражение для силы приобретает вид: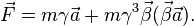

Функция Лагранжа свободной частицы в релятивистской механике:

Запишем интеграл действия, исходя из принципа наименьшего действия: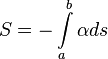

где 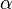-положительное число. Как известно из специальной теории относительности (СТО)

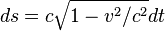, подставляя в интеграл движения, находим:

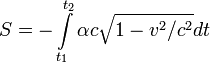. Но, с другой стороны, интеграл движения, можно выразить через функцию Лагранжа: 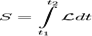. Сравнивая последние два выражения, нетрудно понять, что подынтегральные выражения должны быть равны, то есть:

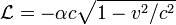Далее, разложим последнее выражение по степеням получим: 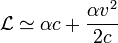, первый член разложения не зависит от скорости, а значит не вносит никаких изменений в уравнения движения. Тогда, сравнивая с классическим выражением функции Лагранжа: 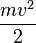, нетрудно определить константу :

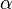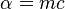.Таким образом, окончательно получаем вид функции Лагранжа свободной частицы: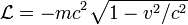

Рассуждения, приведенные выше, можно рассматривать не только для частицы, но и для произвольного тела, лишь бы его части двигались как одно целое.