Закон сохранения энергии в механике

Путь к правильному пониманию переходов движения из одной формы в другую был намечен М.В. Ломоносовым, который сформулировал закон сохранения массы вещества при химических превращениях и закон сохранения материи и движения. Количественную формулировку закона сохранения и превращения энергии дали немецкие ученые Ю. Майер и Г. Гельмгольц (XIX в.): в замкнутой системе энергия может переходить из одних видов в другие и передаваться от одного тела к другому, но ее общее количество остается неизменным.

Закон сохранения и превращения энергии является одним из фундаментальных законов природы, справедливым как для систем макроскопических тел, так и для систем элементарных частиц. Он является выражением вечности и неуничтожимости движения в природе, которое лишь переходит из одной формы в другую.

В замкнутой системе тел, силы взаимодействия между которыми консервативны (потенциальны), отсутствуют взаимные превращения механической энергии в другие виды энергии. Такие системы называются замкнутыми консервативными и для них справедлив закон сохранения энергии в механике: механическая энергия замкнутой консервативной системы не изменяется в процессе ее движения:

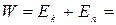const. (3.11)

Для вывода этого закона рассмотрим систему материальных точек максами m₁, m₂, …, m_n, движущихся со скоростями 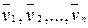. Пусть 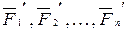- равнодействующие внутренних консервативных сил, действующие на каждую из этих точек, а 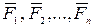- равнодействующие внешних сил, которые также будем считать консервативными. Кроме того, будем считать, что на материальные точки действует еще и внешние неконсервативные силы; равнодействующие этих сил, действующих на каждую из материальных точек, обозначим 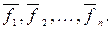При 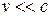массы материальных точек постоянны и уравнения движения этих точек по второму закону Ньютона имеют следующий вид:

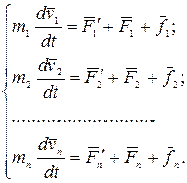(3.12)

Двигаясь под действием сил, точки системы за интервал времени dt совершают перемещения 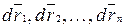. Умножим каждое уравнение системы (3.12) на соответствующее перемещение:

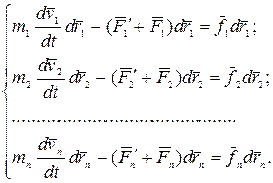
Учитывая, что 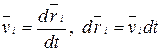, получим:

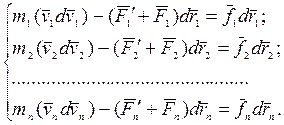
Складывая эти уравнения, получим:

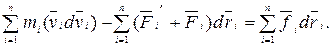(3.13)

Первый член левой части (3.13) представляет собой приращение кинетической энергии системы:

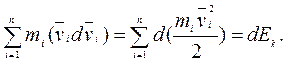
Второй член 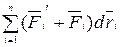равен элементарной работе внутренних и внешних консервативных сил, т.е. равен элементарному приращению потенциальной энергии dE_к.

Правая часть уравнения (3.13) задает работу внешних неконсервативных сил, действующих на систему. Таким образом, имеем:

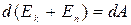(3.14)

При переходе системы из состояния 1 в какое-либо состояние 2

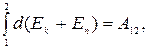
т.е изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними неконсервативными силами. Если внешние неконсервативные силы отсутствуют, то из (3.14) следует, что

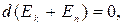
откуда

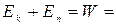const,

что и требовалось доказать.

Закон сохранения механической энергии связан с однородностью времени, т.е. инвариантностью физических законов относительно выбора начала отсчета времени.

Механические системы, на тела которых действуют только консервативные силы (внутренние и внешние), называются консервативными системами. Системы, в которых механическая энергия постепенно уменьшается за счет преобразования в другие виды энергии, называются диссипативными (диссипация – рассеяние энергии). Строго говоря, все системы в природе являются диссипативными и в них закон сохранения механической энергии нарушается. Однако при изменении механической энергии всегда возникает эквивалентное количество энергии другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом состоит физическая сущность закона сохранения и превращения энергии – сущность неуничтожимости материи и ее движения.

Во многих задачах рассматривается одномерное движение тела, потенциальная энергия которого является функцией лишь одной переменной (например, координаты х), т.е. Е_п = f(х). График зависимости потенциальной энергии от некоторого аргумента называется потенциальной кривой, анализ которой позволяет определить характер движения тела.

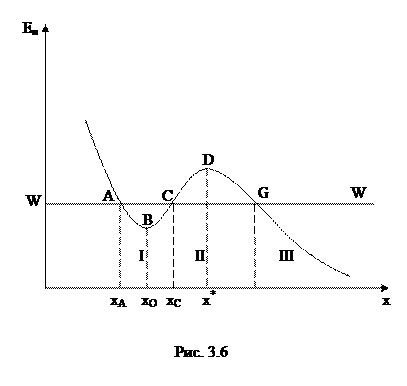В общем случае потенциальная кривая может иметь достаточно сложный вид, например с несколькими максимумами и минимумами (рис. 3.6).

Проанализируем эту потенциальную кривую в предположении, что система консервативна и в ней выполняется закон сохранения энергии в форме (3.11). Если W - заданная полная энергия тела, то тело может находиться только там, где Е_п(х) ≤ W, т.е. в областях I и III. Переходить из области I в область III и обратно тело не может, так как ему препятствует потенциальный барьер CDG, ширина которого равна интервалу значений х, при которых Е_п > W, а его высота определяется разностью Е_пmax-W. Для того чтобы тело смогло преодолеть потенциальный барьер, ему необходимо сообщить дополнительную энергию, равную высоте барьера или превышающую ее. В области I тело с полной энергией W оказывается «запертым» в потенциальной яме ABC и совершает колебания между точками с координатами х_А и х_С.

В точке В с координатой х_О потенциальная энергия тела минимальна. Так как действующая на тело сила 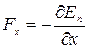, а условие минимума потенциальной энергии 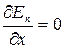, то в точке В F_x =0. При смещении тела из положения х_О в результате малых возмущений в системе оно испытывает действие возвращающей силы, поэтому положение х_О является положением устойчивого равновесия. Указанные условия выполняются и для точки х^* (для Е_пmax). Однако эта точка соответствует положению неустойчивого равновесия, так как при малых возмущениях в системе появляется сила, стремящаяся удалить тело от этого положения. Таким образом, в состоянии устойчивого равновесия замкнутой консервативной системы ее потенциальная энергия имеет минимальное значение, а в состоянии неустойчивого равновесия – максимальное значение.

Рассмотрим применение закона сохранения энергии в механике к расчету абсолютно упругого прямого центрального удара двух шаров. Абсолютно упругим называется такой удар, в результате которого не происходит превращения механической энергии системы соударяющихся тел в другие виды энергии.

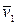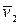Пусть два абсолютно упругих шара массами m₁ и m₂ до удара движутся поступательно со скоростями и , направленными в одну сторону вдоль линии их центров, причем 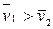(рис. 3.7, а). Требуется найти скорости шаров 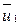и 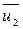после их соударения (рис. 3.7, б).

По закону сохранения энергии в механике имеем:

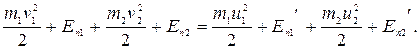(3.15)

Шары движутся в горизонтальной плоскости, поэтому их потенциальная энергия в поле тяготения Земли при ударе не изменяется, т.е.

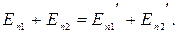
Тогда из уравнения (3.15) получаем:

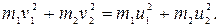(3.16)

С другой стороны, по закону сохранения импульса

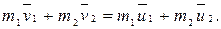(3.17)

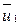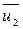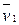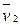При центральном ударе векторы скоростей , , и направлены вдоль одной прямой. Поэтому в уравнении (3.17) можно перейти от векторов к их модулям:

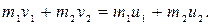(3.18)

Решая совместно уравнения (3.16) и (3.18), получим:

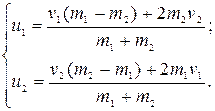(3.19)

Анализ уравнений (3.19) позволяет сделать следующие выводы:

1) Если массы шаров одинаковы (m₁=m₂=m), то 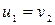и 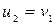, т.е. при ударе шары обмениваются скоростями;

2) если масса второго шара m₂>>m₁, то

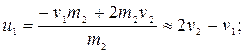
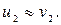
Если при этом второй шар был до удара неподвижен (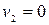), то 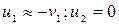, т.е. первый шар отскакивает от неподвижного массивного шара и движется в обратную сторону со скоростью .

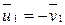Как отмечалось, система тел называется диссипативной, если ее механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии. В качестве примера рассмотрим диссипацию энергии при абсолютно неупругом прямом центральном ударе двух поступательно движущихся шаров (удар называется абсолютно неупругим, если после удара тела движутся как одно целое, т.е. с одной и той же скоростью).

Общая скорость обоих шаров после удара по закону сохранения импульса равна:

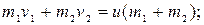
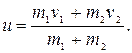(3.20)

Если шары движутся в горизонтальной плоскости, то их потенциальная энергия Е_n остается неизменной. Полная механическая энергия системы до удара

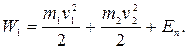
После удара она будет равна

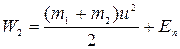, или, с учетом (3.20):

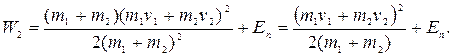
Найдем изменение полной механической энергии системы в результате неупругого удара:

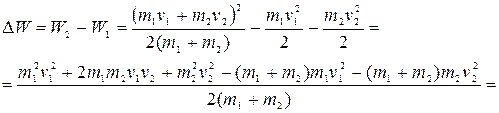
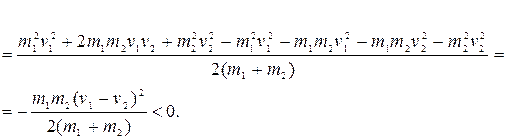
Таким образом, при неупругом ударе полная механическая энергия системы уменьшается, т.е. часть ее рассеивается на деформацию соударяющихся тел. На деформацию тел затрачивается работа, равная убыли полной механической энергии системы:

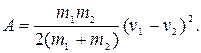
Если второе тело до удара было неподвижн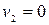о (), то

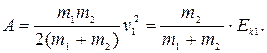(3.21)

Неупругий удар на практике применяется для целей двоякого рода. Во-первых, для изменения формы тела – ковки и штамповки металла, раздробления тел. В этом случае важно, чтобы возможно большая часть кинетической энергии первого тела затрачивалась на работу деформации (формула (3.21)), т.е. чтобы масса неподвижного тела m₂ (например, наковальни вместе с куском металла) была во много раз больше массы ударяющего тела m₁ (например, молота).

Вторая цель состоит в перемещении тел после удара и преодолении при этом сопротивлений (забивка свай в землю, вбивание клиньев и т.п.). В этом случае выгодно, чтобы работа, затрачиваемая на деформацию, была как можно меньше и чтобы общая кинетическая энергия обоих тел после удара (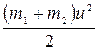) была наибольшей. Для этого необходимо, чтобы масса ударяющего тела m₁ (молота) была во много раз больше массы второго тела m₂ (сваи, гвоздя).

Краткие выводы

· Энергия – универсальная мера различных форм движения материальных объектов и их взаимодействия. Количественной характеристикой процесса обмена энергией между взаимодействующими телами является физическая скалярная величина – работа сил.

Элементарная работа силы

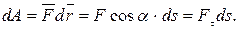
Работа силы на произвольном участке траектории 1-2

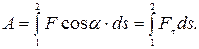
· Мощность – физическая скалярная величина, характеризующая скорость совершения работы:

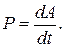
Мощность, развиваемая силой 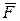в данный момент времени, равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы:

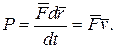
· Консервативная сила – сила, работа которой при перемещении из одного положения в другое не зависит от траектории перемещения, а зависит только от начального и конечного положений тела. Силовое поле, в котором консервативные силы совершают работу, называется потенциальным полем.

· Кинетическая энергия - механическая энергия всякого свободно движущегося тела, численно равная работе, которую совершают действующие на тело силы при его торможении до полной остановки:

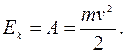
· Потенциальная энергия – это механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.

· Связь между консервативной силой 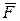и потенциальной энергией устанавливается выражением

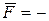grad Е_п,

где

grad Е_п =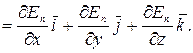

Отсюда, как частные случаи, определяются: а) потенциальная энергия тела массой m на высоте h

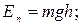
б) потенциальная энергия упругодеформированного тела

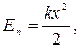
где k – коэффициент упругости (для пружины – жесткость).

· Полная энергия механической системы – равна сумме кинетической и потенциальной энергий:

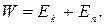
· Механические системы, на тела которых действуют только консервативные силы (внутренние и внешние) называются консервативными системами. В таких системах выполняется закон сохранения механической энергии:

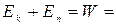const,

т.е. полная механическая энергия консервативной системы со временем не изменяется. Это фундаментальный закон природы, ко торый является следствием однородности времени.

· Система, в которой механическая энергия постепенно уменьшается за счет преобразования в другие формы энергии, называется диссипативной. Строго говоря, все системы в природе являются диссипативными. Однако при уменьшении механической энергии всегда возникает эквивалентное количество энергии другого вида. Другими словами, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом заключается физическая сущность всеобщего закона сохранения и превращения энергии – неуничтожимость материи и ее движения.

Вопросы для самоконтроля и повторения

1. Что такое энергия, работа, мощность?

2. Как определяется работа переменной силы?

3. Какие силы называются консервативными? Приведите примеры консервативных сил.

4. Какие силы называются диссипативными? Приведите примеры таких сил.

5. Дайте определения кинетической и потенциальной энергии.

6. В чем заключается закон сохранения механической энергии? Для каких систем он выполняется?

7. Каким свойством времени обусловлена справедливость закона сохранения механической энергии?

8. В чем физическая сущность закона сохранения и превращения энергии? Почему он является фундаментальным законом природы?

9. Как на основе закона сохранения механической энергии охарактеризовать положения устойчивого и неустойчивого равновесия консервативной системы?

10. Что такое потенциальная яма? потенциальный барьер?

Примеры решения задач

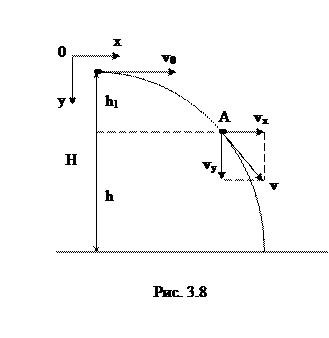
Задача 1. С башни высотой 20 м горизонтально со скоростью 10 м/с брошен камень массой 400 г (рис. 3.8). Пренебрегая сопротивлением воздуха, определить кинетическую и потенциальную энергию камня через 1 с после начала движения.

Дано: H = 20 м; v₀ = 10 м/с; m = 0,4 кг; t = 1c.

Найти: E_k, E_п.

Решение

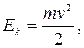
В точке А 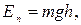где

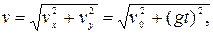
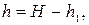
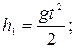
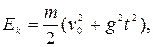
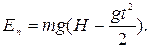
Подставляя числовые данные, получим E_k = 39,2 Дж, E_п = 59,2 Дж.

Ответ: E_k = 39,2 Дж, E_п = 59,2 Дж.

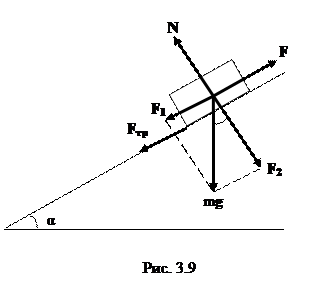Задача 2. Автомобиль массой 1,8 т движется в гору, уклон которой составляет 3 м на каждые 100 м пути (рис. 3.9). Определить: а) работу, совершаемую двигателем автомобиля на пути 5 км, если коэффициент трения равен 0,1; б) развиваемую двигателем мощность, если известно, что этот путь был преодолен за 5 мин.

Дано: m = 1800 кг; sinα = 0,03; s = 5000 м; μ = 0,1; t = 300 с.

Найти: А, Р.

Решение

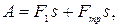где

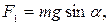
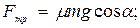
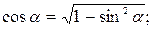
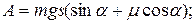
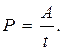
Подставляя числовые данные, получим:

А = 11,5·10⁶ Дж, Р = 38,3·10³ Вт.

Ответ: А = 11,5 МДж, Р = 38,3·кВт.

Задачи для самостоятельного решения

1. Тело массой 5 кг поднимают с ускорением 2 м/с². Определить работу силы в течение первых пяти секунд.

2. Определить работу, совершаемую при подъеме груза массой 50 кг по наклонной плоскости с углом наклона 30⁰ к горизонту на расстояние 4 м, если время подъема составляет 2 с, а коэффициент трения 0,06.

3. С башни высотой 35 м горизонтально брошен камень массой 0,3 кг. Пренебрегая сопротивлением воздуха, определить: а) скорость, с которой брошен камень, если через 1 с после начала движения его кинетическая энергия равна 60 Дж; б) потенциальную энергию камня через 1 с после начала движения.

4. Пуля массой 10 г, летевшая горизонтально со скоростью 500 м/с, попадает в баллистический маятник длиной 1 м и массой 5 кг и застревает в нем. Определить угол отклонения маятника.

5. Тело скользит с наклонной плоскости высотой h и углом наклона α к горизонту и движется далее по горизонтальному участку. Принимая коэффициент трения на всем пути постоянным и равным µ, определить расстояние s, пройденное телом на горизонтальном участке, до полной остановки.

6. Автомобиль массой 1,8 т спускается при выключенном двигателе с постоянной скоростью 54 км/ч по наклонной плоскости (угол к горизонту 3⁰). Определить, какой должна быть мощность двигателя автомобиля, чтобы он смог подняться на такой же подъем с той же скоростью.

7. Камень массой 0,2 кг бросили под углом 60⁰ к горизонту со скоростью 15 м/с. Найти кинетическую, потенциальную и полную энергию камня: а) спустя 1 с после начала движения; б) в высшей точке траектории. Сопротивлением воздуха пренебречь.

8. Тело массой 5 кг падает с высоты 20 м. Определить полную энергию тела в точке, находящейся от поверхности Земли на высоте 5 м. Трением тела о воздух пренебречь. Сравнить эту энергию с первоначальной энергией тела.

9. Тело, падая с некоторой высоты, в момент соприкосновения с Землей обладает импульсом 100 кг·м/с и кинетической энергией 500 Дж. Определить: а) с какой высоты тело падало; б) массу тела.

10. Тело брошено под углом 45⁰ к горизонту со скоростью v₀ =15 м/с. Используя закон сохранения энергии, определить скорость тела в высшей точке его траектории.

ГЛАВА 4. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

ТВЕРДОГО ТЕЛА