Свойства допустимого множества и оптимального решения в задаче ЛП

Стандартная (нормальная) и каноническая формы представления задачи ЛП и сведение к ним.

Математическая модель ЗЛП может быть канонической и неканонической.

Если все ограничения системы заданы уравнениями и переменные 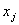неотрицательные, то такая модель задачи называется канонической. Если хотя бы одно ограничение является неравенством, то модель ЗЛП является неканонической. Чтобы прейти от неканонической модели к канонической, необходимо в каждое неравенство ввести балансовую переменную 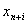. Если знак неравенства ≤, то балансовая переменная вводится со знаком +, если знак неравенства ≥, то со знаком -. В целевую функцию балансовые переменные не вводятся.

Свойства допустимого множества и оптимального решения в задаче ЛП.

Определение. Допустимым планом (допустимым решением) задачи линейного программирования называется вектор 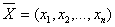, удовлетворяющий системе ограничений. Множество допустимых решений образует область допустимых решений.

Допустимое решение, при котором целевая функция достигает своего экстремального значения, называется оптимальным решением ЗЛП и обозначается .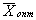

1.Выпуклые множества в n-мерном пространстве.

Рассмотрим на плоскости Х₁ОХ₂ совместную систему линейных неравенств

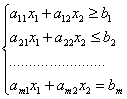
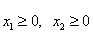
Каждое неравенство этой системы геометрически определяет полуплоскость с граничной прямой 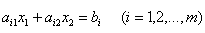. Условия неотрицательности определяют полуплоскости соответственно с граничными прямыми 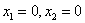. Система совместна, поэтому полуплоскости как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых являются решением данной системы. Совокупность этих точек называется многоугольником решений. Он может быть точкой, отрезком, лучом, многоугольником, неограниченной многоугольной областью.

2.Свойства решений задачи линейного программирования.

Теорема 1. Множество всех планов задачи линейного программирования выпукло.

Теорема 2. Целевая функция задачи линейного программирования может достигать экстремального значения только в угловой точке области допустимых решений.

Таким образом, для нахождения оптимального решения задачи линейного программирования нет необходимости перебирать все допустимые решения, а достаточно ограничиться перебором лишь конечного числа возможных решений угловых точек многоугольника.