Графический метод решения ЗЛП

Наиболее простым и наглядным методом решения ЗЛП является графический метод. Он основан на геометрической интерпретации ЗЛП и применяется при решении ЗЛП с двумя переменными.

Алгоритм графического метода решения ЗЛП.

1. Строится область допустимых решений (ОДР) ЗЛП.

2. Строится вектор-градиент 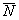целевой функции с началом в точке О(0,0).

3. Проводится линия уровня, которая перпендикулярна вектору .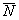

4. Линия уровня перемещается по направлению вектора 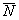для задач на максимум и в направлении, противоположном 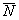для задач на минимум. Перемещение производится до тех пор, пока у нее не окажется только одна общая точка с областью допустимых решений. Эта точка, определяющая единственное решение ЗЛП, и будет точкой экстремума. Если окажется, что линия уровня параллельна одной из сторон ОДР, то в таком случае экстремум достигается во всех точках соответствующей стороны, а ЗЛП будет иметь бесчисленное множество решений. ЗЛП может быть неразрешимой, когда определяющие ее ограничения окажутся противоречивыми.

5. Находим координаты точки экстремума и значение целевой функции в ней.

1. Построение опорных планов.

Симплексный метод является универсальным, т.е. может быть применен при решении любой задачи линейного программирования.

В основе симплексного метода лежит алгоритм симплексных преобразований системы. Он позволяет, исходя из известного опорного плана (базисного решения) задачи, за конечное число шагов получить ее оптимальный план.

Идея симплексного метода содержит три существенных момента:

- указывает способ нахождения первоначального опорного плана;

- устанавливает критерий оптимальности опорного плана;

- указывает способ перехода от неоптимального плана к лучшему плану, более близкому к оптимальному.

Таким образом, идея симплекс – метода заключается в последовательном улучшении плана.

Решение ЗЛП симплекс-методом проводится в симплексных таблицах, которые заполняются после нахождения исходного базисного (опорного) решения. Общий вид симплексной таблицы:

Базис	СБаз.	В	С1	С2	…	Ск	Ск+1	…	Сj	…	Cn
	х1	х2	…	хк	хк+1	…	хj	…	хn
Х1	C1	b1			…		a1,k+1	…	a1j	…	a1n
х2	C2	b2			…		a2,k+1	…	a2j	…	a2n
…	…	…	…	…	…	…	…	…	…	…	…
хk	Ck	bk			…		ak,k+1	…	akj	…	akn
Δj	Z0			…		Δk+1	…	Δj	…	Δn

2. Отыскание оптимального плана. Условия оптимальности.

Теорема. Если после выполнения очередной итерации:

1) найдется хотя бы одна отрицательная оценка Δ_j для задачи на max(положительная для задачи на min) и в каждом столбце с такой оценкой будет хотя бы один положительный элемент, то можно улучшить план, выполнив следующую итерацию;

2) найдется хотя бы одна отрицательная (положительная) оценка, столбец которой не содержит положительных элементов, то функция Z неограничена в области допустимых решений, т.е. ;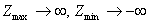

3) все оценки окажутся неотрицательными для задач на max (не положительными для задач на min), то найдено оптимальное решение.

3.Алгоритм симплексного метода.

Математическая модель задачи должна быть канонической. Если она неканоническая, то ее надо привести к каноническому виду. Исходная задача должна содержать базисные переменные, т.е. вектора образующие единичную матрицу.

Для задачи на определения максимума.

Шаг 1. Заполняем первую симплекс-таблицу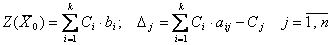

Шаг 2. Проверяем план на оптимальность: все .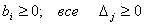

а) план оптимален, то выписываем решение,

б) задача неразрешима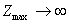

в) иначе переходим к шагу 3.

Шаг 3. Выбираем разрешающий столбец: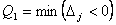

Шаг 4. Выбираем разрешающую стороку: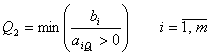

Шаг 5. На пересечение разрешающего столбца и строки стоит разрешающий элемент. В базисе вектор стоящий в разрешеющей строке заменяем на вектор стоящий в разрешающем столбце.

Шаг 6. Пересчитываем новую симплекс- таблицу по методу Жордана-Гаусса.

В задаче на определение минимума изменяются следующие шаги.

Шаг 2. Проверяем план на оптимальность: все .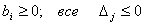

а) план оптимален, то выписываем решение,

б) задача неразрешима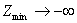

в) иначе переходим к шагу 3.

Шаг 3. Выбираем разрешающий столбец: .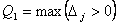

Алгоритм метода Жордана-Гаусса:

1. Разрешающая строка делится на разрешающий элемент.

2. Разрешающий столбец дополняется нулями.

3. Если в разрешающей строке (столбце) имеются нули, то соответствующие им столбцы (строки) переписываются без изменения.

4. Остальные элементы вычисляются по правилу «прямоугольника»: Новый элемент равен разности произведений чисел, стоящих по диагоналям, деленной на разрешающий элемент, причем первое произведение берется с разрешающим элементом: