Сумма вероятностей событий, которые образуют полную группу, равна единице. Грубо говоря, если события образуют полную группу, то со 100%-й вероятностью какое-то из них произойдёт. В самом простом случае полную группу образуют противоположные события, например:
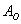 – в результате броска монеты выпадет орёл;
– в результате броска монеты выпадет орёл;
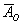 – в результате броска монеты выпадет решка.
– в результате броска монеты выпадет решка.
По теореме: 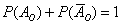
Совершенно понятно, что данные события равновозможны и их вероятности одинаковы 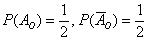 .
.
По причине равенства вероятностей равновозможные события часто называют равновероятными. А вот и скороговорка на определение степени опьянения получилась =)
Пример с кубиком: события 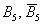 противоположны, поэтому
противоположны, поэтому 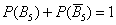 .
.
Рассматриваемая теорема удобна тем, что позволяет быстро найти вероятность противоположного события. Так, если известна вероятность 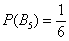 того, что выпадет пятёрка, легко вычислить вероятность того, что она не выпадет:
того, что выпадет пятёрка, легко вычислить вероятность того, что она не выпадет:
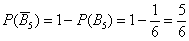
Это гораздо проще, чем суммировать вероятности пяти элементарных исходов. Для элементарных исходов, к слову, данная теорема тоже справедлива:
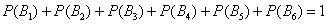
События 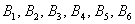 , как отмечалось выше, равновозможны – и теперь мы можем сказать, что равновероятны. Вероятность выпадения любой грани кубика равна
, как отмечалось выше, равновозможны – и теперь мы можем сказать, что равновероятны. Вероятность выпадения любой грани кубика равна 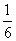 :
:
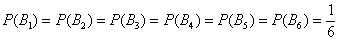
Ну и на закуску колода: поскольку нам известна вероятность 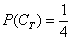 того, что будет извлечена трефа, то легко найти вероятность того, что будет извлечена карта другой масти:
того, что будет извлечена трефа, то легко найти вероятность того, что будет извлечена карта другой масти:
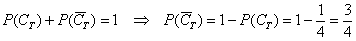
Заметьте, что рассмотренные пары событий 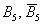 и
и 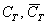 не равновероятны, как оно чаще всего и бывает.
не равновероятны, как оно чаще всего и бывает.
В упрощенной версии записи решения вероятность противоположного события стандартно обозначается строчной буквой 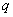 . Например, если
. Например, если 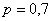 – вероятность того, что стрелок попадёт в цель, то
– вероятность того, что стрелок попадёт в цель, то 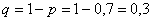 – вероятность того, что он промахнётся.
– вероятность того, что он промахнётся.
! В теории вероятностей буквы 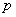 и
и 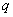 нежелательно использовать в каких-то других целях.
нежелательно использовать в каких-то других целях.
 2015-03-20
2015-03-20 1496
1496








