Основные понятия теории вероятностей

Основные понятия теории вероятностей. Классическое определение вероятности. Элементы комбинаторики.

Теория вероятностей (ТВ) – математическая наука, изучающая закономерности в случайных явлениях.

Предметом теории вероятностей является изучение количественных закономерностей массовых однородных случайных событий.

Знание закономерностей, которым подчиняются массовые случайные события, позволяет предвидеть, как эти события будут протекать.

Методы теории вероятностей широко применяются в различных отраслях естествознания и техники: в теории надежности, теории массового обслуживания, теоретической физики, геодезии, астрономии, теории стрельбы, теории ошибок наблюдений, теории автоматического управления, общей теории связи, и во многих других теоретических и прикладных науках. Теория вероятностей служит также для обоснования математической и прикладной статистики, которая в свою очередь используется при планировании и организации производства, при анализе технологических процессов, предупредительном и приемочном контроле качества продукции и для многих других целей.

Таким образом, ТВ изучает математическую модель опыта (эксперимента) исход которого предсказать не удается.

При этом под опытом (экспериментом, испытанием) понимают некоторую совокупность действий, которая может быть повторена в однотипных (неизменных основных) условиях неограниченное число раз.

Комплекс второстепенных условий, которые не возможно проконтролировать, изменяется от опыта к опыту, что и приводит к различным результатам.

Событием называется всякий факт, который в результате опыта может произойти или не произойти.

Обозначаются события заглавными буквами латинского алфавита: A, B, C.

Пример 1: опыт – бросок монеты,

основные условия – симметричность монеты,

второстепенные условия – сила броска, скорость ветра, влажность и т.д.,

события – выпадение " (орла" или "решки".

опыт – проведение лекции,

основные условия – периодичность, место проведения, лектор,

второстепенные условия – рабочая неделя, наличие мультимедийной установки в аудитории,

событие – присутствие студента на лекции.

Элементарным событием называется один из взаимоисключающих друг друга исходов опыта.

Обозначаются элементарные события малыми буквами латинского или греческого алфавитов: a,b,c, ά, β, ω.

Множество всех элементарных событий называется пространством элементарных событий. При этом каждому исходу опыта ставится в соответствие лишь одна точка из этого пространства (множества).

Обозначается пространство элементарных событий Ω.

Наблюдаемые нами явления (события) можно разделить на три вида:

достоверные,

невозможные,

случайные.

Достоверным называется событие, которое в результате опыта непременно должно произойти (обозначается: U).

Невозможным называется событие, которое в результате опыта не может произойти (обозначается: Ø).

Случайным называется событие, которое при многократном повторении опыта в одних исходах происходит, а в других – нет.

Для всякого случайного события A и каждого элементарного события ω можно сказать, благоприятно (влечет) ли элементарное событие ω для наступления случайного события А или нет.

Пример 2: Рассмотрим эксперимент однократное подбрасывание монеты.

Опыт: бросок монеты.

Элементарные события: ω₁ – выпадение герба (Г),

ω₂ – выпадение цифры (Ц).

Пространство элементарных событий: Ω = {}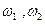

Случайные события: А₁ – выпала Ц, А₁= {},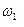

А₂ – выпал Г, А₂= {}.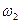

Таким образом, эл. с. ω₁ благоприятно сл.с. А₁, а эл. с. ω₂ благоприятно сл.с. А_2.

Пример 3: Однократное подбрасывание игральной кости.

Опыт: бросок кости.

Элементарные события: ω₁ – выпало одно очко,

ω₂ – выпало два очка,

. ω₃ – выпало три очка,

ω₄ – выпало четыре очка,

ω_5, ω₆ – выпадение пяти и шести очков соответственно.

Пространство элементарных событий: Ω = {}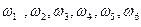

Случайные события: А – выпало четное число очков, А= {},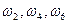

В – выпало нечетное число очков, В= {},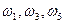

С – выпало семь очков, С=Ø,

D – выпало не более шести очков, D= {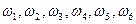}= U.

События называют несовместными, если никакие два из них не могут произойти одновременно в одном опыте

Пример 4: Появление герба и появление цифры при подбрасывании 1-ой монеты.

– Появление четного и нечетного числа очков при одном подбрасывании кубика.

Примером совместныхсобытий является выпадение одного очка и нечетного числа очков.

Полной группой событий называются несколько попарно несовместных событий таких, что в результате опыта одно из них непременно должно произойти.

Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие.

Пример 5: Появление герба и появление цифры при подбрасывании 1-ой монеты

Появление черной и красной масти при вытягивании карты из колоды

Если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий.

События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другие.

Пример 6: Опыт: подбрасывание монеты. События: появление герба и появление цифры.

Примером неравновозможных событий является выпадение двух очков и нечетного числа очков.

Если исходы опыта образуют полную группу несовместных равновозможных событий, то они называются случаями

При однократном броске игрального кубика случаями являются исходы, которые заключаются в выпадении:

– 1, 2, 3, 4, 5, 6 очков;

– четного и нечетного числа очков.