Пусть 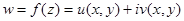 - непрерывная функция комплексного переменного z, определенная в некоторой области и L – кривая, лежащая в этой области.
- непрерывная функция комплексного переменного z, определенная в некоторой области и L – кривая, лежащая в этой области.
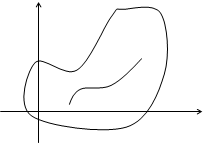 у
у
В
L
А
х
Кривая L задана уравнением 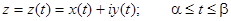
Определение. Интеграл от функции f(z) вдоль кривой L определяется следующим образом:
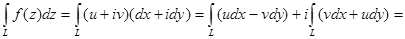
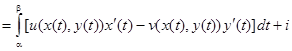
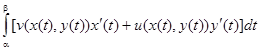
Если учесть, что 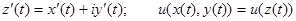 , то
, то
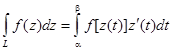
Теорема. (Теорема Коши) Если f(z) - аналитическая функция на некоторой области, то интеграл от f(z) по любому кусочно – гладкому контуру, принадлежащему этой области равен нулю. 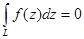
 2015-03-20
2015-03-20 492
492








