Определение. Трансцендентными называются аналитические функции, которые не являются алгебраическими.
Если аргументом показательной или тригонометрических функций является комплексное число, то определение этих функций, вводимое в элементарной алгебре теряет смысл.
Рассмотрим разложение в степенной ряд следующих функций:
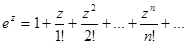
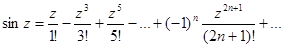
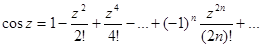
Функции ez, cosz, sinz связаны между собой формулой Эйлера. Эта формула может быть очень легко получена сложением соотвествующих рядов.
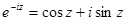
Также справедливы равенства: 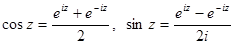
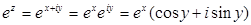
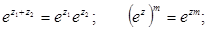
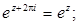
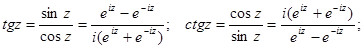
Для тригонометрических функций комплексного аргумента справедливы основные тригонометрические тождества (синус и косинус суммы, разности и т.д.), которые справедливы для функций действительного аргумента.
Определение. Гиперболическим синусом, косинусом, тангенсом и котангенсом называются соответственно функции:
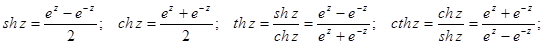
Гиперболические функции могут быть выражены через тригонометрические: 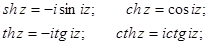
Гиперболические функции sh z и ch z имеют период 2pi, а функции th z и cth z – период pi.
Пример. Найти sin(1+2i).
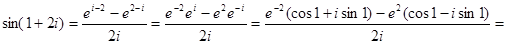
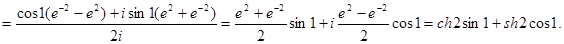
Определение. Логарифмическая функция комплексного аргумента определяется как функция, обратная показательной.
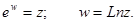
Если w = u + iv, то 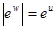 и Arg ew =
и Arg ew = 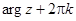 = v.
= v.
Тогда eu = 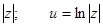 .
.
Итого: 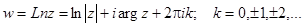
Для комплексного числа z = a + ib 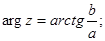
Определение. Выражение 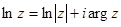 называется главным значением логарифма.
называется главным значением логарифма.
Логарифмическая функция комплексного аргумента обладает следующими свойствами:
1) 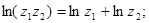
2) 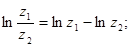
3) 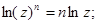
4) 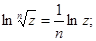
Обратные тригонометрические функции комплексного переменного имеют вид:
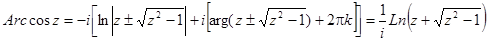
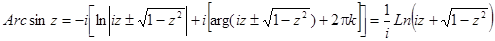
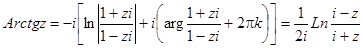
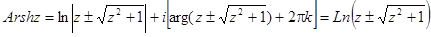
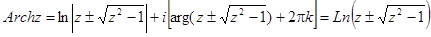
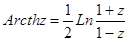
 2015-03-20
2015-03-20 4644
4644
