2015-03-20
1546
Между основными показателями надежности существуют аналитические зависимости, которыми удобно пользоваться при оценке какого-то конкретного показателя при известном другом.
Вероятность безотказной работы P (t) и средняя наработка до отказа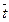 
:
,
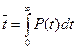т.е. средняя наработка до отказа невосстанавливаемого объекта равна площади под кривой P (t).
Вероятность безотказной работы P (t)и интенсивность отказов λ(t)
.
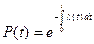Интенсивность отказов λ(t)и средняя наработка до отказа 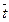при постоянной интенсивности отказов 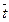=1/λ, что характерно для внезапных отказов при экспоненциальном законе распределения средней наработки до отказа.
Вероятность безотказной работы P (t), интенсивность отказов λ(t) и средняя наработка до отказа 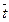при том же условии: 
.
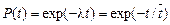Средняя наработка на отказ восстанавливаемого объекта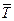 
и параметр потока отказов ω(t) 
.
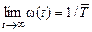Независимо от закона распределения времени безотказной работы, параметр потока отказов стремится к постоянной величине, обратной средней наработки на отказ.
Вероятность восстановления P (t в) и интенсивность восстановления μ(t в):
.
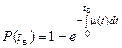Вероятность безотказной работы P (t с)и средний срок службы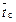 
:
P (t) = 1–φ((t – 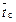) / σ),
где φ – функция Лапласа; σ – дисперсия нормального распределения среднего срока службы, что характерно для постепенных отказов при нормальном законе распределения среднего срока службы (или средней наработки до отказа).
