В дальнейшим будем использовать в математических моделях материалов систему обозначений физических величин, представленную в таблице 4.1
Таблица 1 - Система обозначений физических величин
| Обозначение | Определение |
| { εel } | упругие деформации |
| { εpl } | пластические деформации |
| { εtr } | пробные деформации |
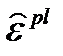 | эквивалентные пластические деформации |
| { σ } | напряжения |
| σe | эквивалентные напряжения |
| σy | предел текучести материала |
| σm | величина гидростатических напряжений |
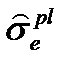 | эквивалентные пластические напряжения |
| λ | пластический коэффициент (определяет величину пластических деформаций) |
| { α } | перемещение поверхности текучести |
| κ | пластическая работа |
| C | множитель перемещения (параметр материала) |
| [ D ] | матрица напряжений-деформаций |
| ET | касательный модуль |
| F | критерий текучести |
| N | коэффициент напряжений |
| Q | потенциал пластической деформации (функция напряжений, определяющая направление пластических деформаций) |
| { S } | девиаторные напряжения |
Для описания поведения материала с пластичностью, не зависящей от скорости деформации, необходимо иметь математические соотношения, определяющие три типа параметров:
- критерий текучести;
- закон текучести;
- закон упрочнения.
Критерий текучести определяет уровень напряжений при котором в материале начинаются пластические деформации. Для сложного напряженного состояния он является функцией всех компонентов вектора напряжений f ({ σ }), которая обычно представляется как эквивалентные напряжения σe:
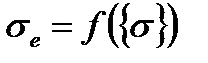 . (4.4)
. (4.4)
В случае, если эквивалентные напряжения в материале равны пределу текучести материала σy:
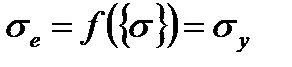 , (4.5)
, (4.5)
в материале начинаются пластические деформации. Пока эквивалентные напряжения меньше, чем предел текучести, материал остается упругим, и напряжения подчиняются упругой зависимости между напряжениями и деформациями. Заметим, что в рассматриваемой теории пластичности эквивалентные напряжения не могут превышать напряжения текучести материала, ведь при его достижении пластические деформации происходят мгновенно и не позволяют напряжениям превысить предел текучести. Само выражение (4.5) может быть графически представлено в виде поверхностей напряжений (рисунок 4.2) различных для разных моделей пластичности. Поверхности на рисунке 4.2 называются поверхностями текучести т.к. любое напряжение внутри них является упругим и не приводит к появлению пластических деформаций.
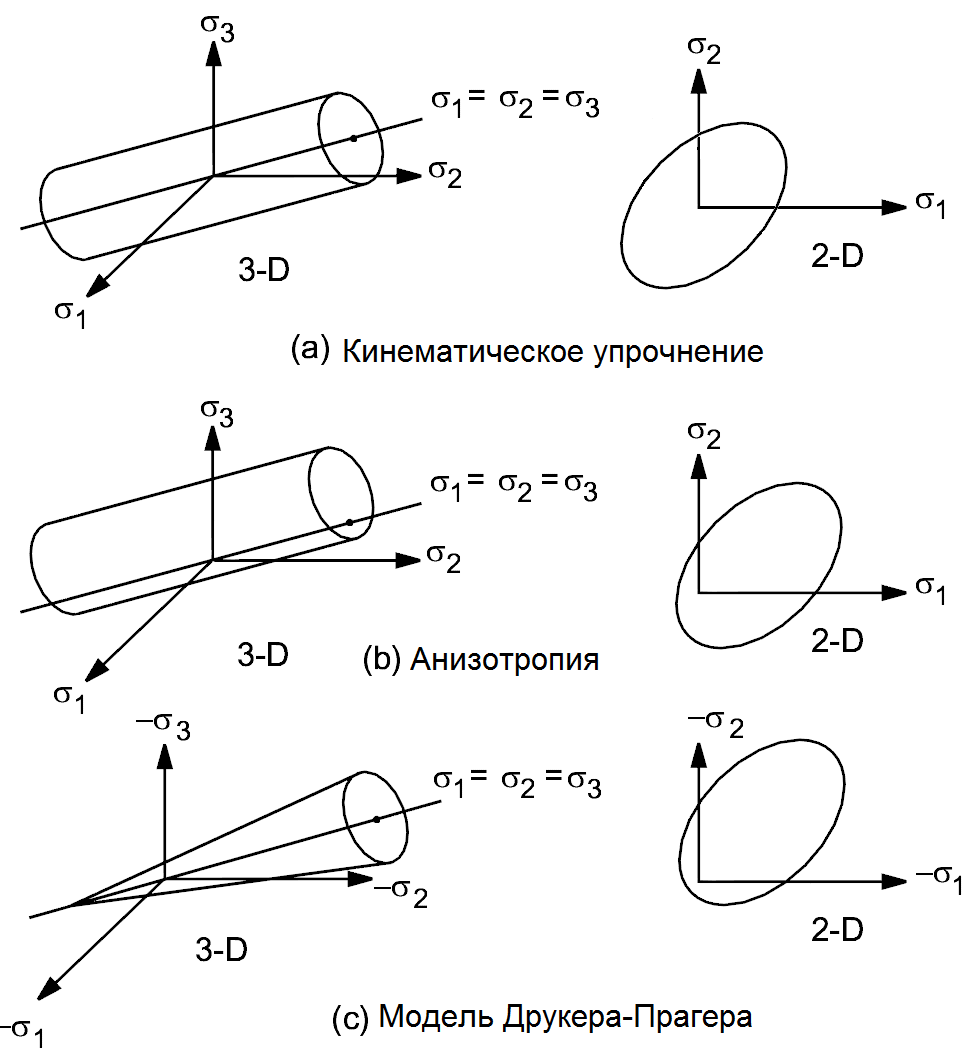
Рисунок 4.2 - Поверхности текучести для различных моделей пластичности
Закон текучести определяет направление пластических деформаций и записывается в следующем виде:
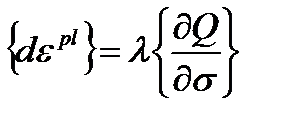 . (4.6)
. (4.6)
Если Q есть функция текучести (как обычно и подразумевается) т.е. то Q = F, закон текучести называют ассоциированным, а пластические деформации происходят перпендикулярно поверхности текучести.
Закон упрочнения описывает изменение поверхности текучести при неоднократном пластическом нагружении и позволяет определить условия (т.е. напряженное состояние) повторного возникновения пластических деформаций. Существует два типа законов упрочнения: механическое упрочнение (деформационное упрочнение, наклёп) и кинематическое упрочнение. При механическом упрочнении поверхность текучести не меняет своей начальной оси, но увеличивается в размере в связи с развитием пластических деформаций. Для материалов с изотропной пластичностью такое упрочнение называется изотропным (рисунок 4.3 а). Кинематическое упрочнение подразумевает, что размер поверхности текучести не меняется, но сама она сдвигается в пространстве напряжений, как показано на рисунке 4.3 б.
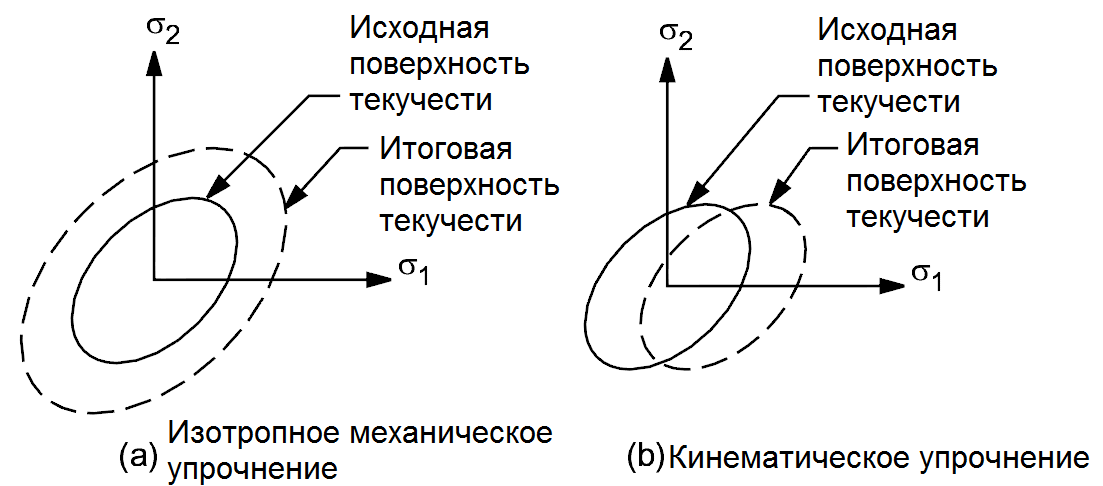
Рисунок 4.3 - Типы законов упрочнения
 2015-03-20
2015-03-20 993
993








