Билет 17

1. Уравнение годографа МОВ и МОВ ОГТ однократных волн.

Принципиальную сущность МОГТ составляет идея многократного прослеживания одних и тех же отраженных волн при различном взаимном положении источников и приемников упругих колебаний. Широкое применение систем многократных перекрытий в практике сейсморазведочных работ обусловлено возможностью реализации в процессе обработки алгоритмов, обеспечивающих существенное повышение сигнал/помеха за счет ослабления как нерегулярных колебаний, так и регулярных волн-помех типа кратных, обменных и др.

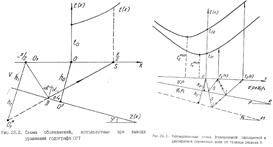
В основу большинства таких алгоритмов заложены кинематические особенности отраженных (однократных и многократных) и дифрагированных волн. Кроме того, кинематические характеристики сейсмических волн, регистрирующихся на сейсмограмме ОГТ, играют важную роль при расчетах и выборе параметров систем наблюдений. Сейсмограммы (с/г), обрабатываемые по методике ОГТ, представляют собой выборку каналов (трасс) из сейсмограммы общей точки возбуждения (ОТВ), полученных в процессе многократного профилирования. Годографы сейсмических волн, прокоррелированные (выделенные) на сейсмограмме ОГТ в соответствии с принципами симметрии относительно центра расстановки – общей средней точки (ОСТ) называют годографами ОГТ. График, выражающий зависимость времени t прихода волны от координат x и y точек наблюдения называют годографом. Пусть плоская отражающая граница залегает под углом φ к горизонту. Покрывающая ее толща однородна и характеризуется всюду одинаковой скоростью V. Начало координат разместим в точке О, которую будем называть общей средней точкой (ОСТ). Глубину по нормали от центра системы наблюдений до границы раздела примем равной h_0. В точке на профиле наблюдений, имеющей координату минус х/2, поместим источник колебаний. В точке профиля х/2 (расположенной симметрично относительно ОСТ) поместим приемник колебаний. Требуется определить время пробега отраженной волны от источника до приемника. Эту зависимость, полученную в виде формулы, будем называть уравнением годографа ОГТ. При выводе искомой формулы будем использовать уже известное нам уравнение годографа отраженной волны для общей точки взрыва ОТВ. Для этого временно совместим начало новой системы координат с пунктом взрыва О₁. Глубина по нормали до отр.границы в этой точке профиля равна

h₁=h₀-x/2sin φ. (1)

Как известно, уравнение годографа ОТВ, определяющее время пробега волны по траектории О₁DS, в этой системе координат и обозначений будет иметь вид:

t(x)=1/V*√x²+4h₁x sin φ +4h₁² (2).- МОВ

Подставив в ур-е (2) глубину h₁ из (1), будем иметь:

t(x)=1/V*√x²+4x (h₀-x/2 sin φ) sin φ+4(h₀-x/2 sin φ)² = 1/V*√x² - х²sin² φ+4h₀² =1/V*√4 h₀² + х²cos² φ (3).

После внесения под знак радикала и с учетом нижеследующих общепринятых обозначений: t₀=2h₀ / V; V_огт= V/cosφ (4) будем иметь следующее окончательное выражение для уравнения годографа ОГТ

t(x)= √ t₀² + x²/V_огт² -МОВ ОГТ

Следует всегда помнить, что х – расстояние от ПВ до ПП. Из анализа уравнения годографа ОГТ следуют такие важные выводы: годограф ОГТ однократно отраженной волны для однородной покрывающей среды представляет собой гиперболу с мин. в точке симметрии – точке ОСТ; - С увеличением угла наклона отражающей границы крутизна годографа уменьшается; - форма годографа не зависит от знака угла наклона отражающей границы; - для фиксированного t₀ годограф ОГТ является функцией только одного параметра – параметра Vогт, который принято называть скоростью ОГТ, фиктивной скоростью и т. п.

Волны Р и S распространяющиеся от источника вниз и отразившиеся от границы, наз-т однократно-отраженными (отраженными). Нижние точки отражения могут соответствовать одной и той же границе – полнократная волна.

2. Намагниченность: ее природа и носители. Виды намагниченности.

Источник намагниченности – магнитные свойства горных пород, которые основаны на спиновых и орбитальных моментах электронов.

При наведении поля электроны упорядочиваются:

Намагниченность определяется как отношение суммы магнитных моментов к сумме элементарных объемов вещества.

,

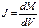Где М – магнитный момент, V – объем. [J]=A/м (СИ), в (Сгс) размерности не имеет. J_СИ=10³J_СГС

Если направление модуль-вектора J постоянно, то намагниченность однородная.

Виды намагниченности:

1. Индуктивная или наведенная намагниченность (вызвана внешним полем и исчезает при его снятии). Обозначается J_i

2. Остаточная намагниченность (характерна для ферромагнетиков, т.е. остается при снятии поля). Обозначается J_n

Характеристика магнитных свойств вещества:

Q=Jn/Ji – коэффициент Кёнигсбергера (им характеризуется естественная остаточная намагниченность)

3. Основные уравнения Максвелла для переменного тока, их характеристика.

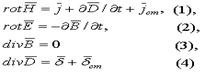
Первое уравнение – дифференциальное выражение закона полного тока, указывает на связь вихревого магнитного поля с токами проводимости и смещения. Второе уравнение – дифференциальное выражение закона электромагнитной индукции – всякое изменение магнитной индукции В возбуждает в проводящей среде вихревое электрическое поле Е. Направление вихря Е таково, что возникший индукционный ток и связанное с ним вторичное магнитное поле противодействуют изменению магнитной индукции, на что указывает знак минус. Третье и четвёртое уравнения выражают непрерывность (замкнутость) магнитных и электрических силовых линий в отсутствие сторонних зарядов.