Предприятие должно определить уровень выпуска продукции и предоставления услуг на некоторый период времени, так, чтобы удовлетворить потребности клиентов. Точная величина спроса на продукцию и услуги неизвестна, но ожидается, что в зависимости от соотношения сил на рынке товаров, действий конкурентов и погодных условий, спрос может принять одно из четырех возможных значений: 300, 400, 500 или 600 изделий. Маркетинговые исследования позволили определить возможные вероятности возникновения этих ситуаций, которые соответственно составили 0,2; 0,4; 0,3 и 0,1. Для каждого из возможных значений спроса существует наилучший уровень предложения, с точки зрения возможных затрат и прибыли, отклонение от этих уровней связано с риском и может привести к дополнительным затратам либо из-за превышения предложения над спросам, либо из-за неполного удовлетворения спроса. В первом случае это связано с необходимостью хранения нереализованной продукции и потерями при реализации ее по сниженным ценам, во втором – с дополнительными затратами по оперативному выпуску недостающей продукции, т.к. иначе это будет связано с риском потери клиентов. Данную ситуацию можно представить в виде матрицы игры (табл.1)
Таблица 1
Анализ стратегий производства при неопределенной
рыночной конъюнктуре
| Объем предложения | Возможные колебания спроса на продукцию | |||
| П1 = 300 | П2 = 400 | П3 = 500 | П4 = 600 | |
| Вероятность состояния спроса | ||||
| q1 = 0,2 | q2 = 0,4 | q3 = 0,3 | q4 = 0,1 | |
| Размер прибыли (убытков) в зависимости от колебаний спроса (аij) | ||||
| С1 = 300 | ||||
| С2 = 400 | ||||
| С3 = 500 | -18 | |||
| С4 = 600 | -42 | -8 |
Для выбора наилучшей стратегии поведения на рынке товаров и услуг существуют различные критерии, среди которых можно назвать критерии: Байеса, Лапласа, Вальда, Сэвиджа, Гурвица и максимакса. Считается, что вернее будет выбрать ту стратегию, которая будет предпочтительнее по нескольким критериям.
По критерию Байеса наилучшая стратегия определяется выражением:
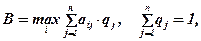
где aij - размер "выигрыша" при выборе i-й стратегии при j-м состоянии "природы"; qj - вероятность возникновения j-го состояния "природы".
В1 = 30 * 0,2 + 22 * 0,4 + 16 * 0,3 + 8 * 0,1 = 20,4
В2 = 6 * 0,2 + 40 * 0,4 + 32 * 0,3 + 24 * 0,1 = 29,2
В3 =-18 * 0,2 + 16 * 0,4 + 50 * 0,3 + 42 * 0,1 = 22,0
В4 =-42 * 0,2 - 8 * 0,4 + 36 * 0,3 + 60 * 0,1 = 4,8
Наилучшая стратегия В2 дает максимальный "выигрыш" в размере 29,2.
По критерию Лапласа:
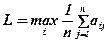
L1 = (30 + 22 + 16 + 8)/4 = 19
L2 = (6 + 40 + 32 + 24)/4 = 25,5
L3 = (-18 + 16 + 50 + 42)/4 = 22,5
L4 = (-42 - 8 + 36 + 60)/4 = 11,5
Наилучшая стратегия L2 дает максимальный "выигрыш" в размере 25,5.
По критерию Вальда:
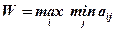
W1 = 8; W2 = 6; W3 = -18; W4 = -42.
Наилучшая стратегия W1 дает максимальный "выигрыш" в размере 8.
По критерию Сэвиджа наилучшая стратегия соответствует минимальному риску:
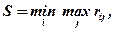
где rij - размер риска при выборе i-й стратегии при j-м состоянии "природы";
rij = 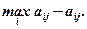
r11 = 30 - 30 = 0; r12 = 40 - 22 = 18; r21 = 30 - 6 = 24 и т.д., в результате получаем матрицу рисков.
Матрица рисков
| Стратегии | Состояния «природы» | 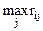 | |||
| П1 = 300 | П2 = 400 | П3 = 500 | П4 = 600 | ||
| С1 = 300 | |||||
| С2 = 400 | 36 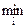 | ||||
| С3 = 500 | |||||
| С4 = 600 |
Наилучшая стратегия S2 дает минимальный риск.
По критерию Гурвица:
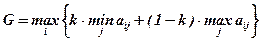
где k - коэффициент "пессимизма", примем k = 0,3.
G1 = 0,3 * 8 + 0,7 * 30 = 23,4
G2 = 0,3 * 6 + 0,7 * 40 = 29,8 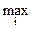
G3 = 0,3 * (-18) + 0,7 * 50 = 29,6
G4 = 0,3 * (-42) + 0,7 * 60 = 29,4.
Наилучшая стратегия G2 дает "выигрыш" 29,8.
По критерию максимакса:
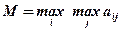
Наивыгоднейшая стратегия может дать "выигрыш" в размере 60, но ей же соответствует и наибольший риск (72).
По большинству критериев наилучшая стратегия С2 = 400 изделий.
ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ
"УТВЕРЖДАЮ"
Декан факультета
__________ Дорофеев Э.Б.
"___"________2006 г.
РАБОЧАЯ ПРОГРАММА
по дисциплине "Методы и модели в экономике"
для студентов экономических
специальностей всех форм обучения
Факультет: Инженерно-экономический
Кафедра: Экономики, производственного
менеджмента и организации
машиностроительного производства
ВОРОНЕЖ - 2006
Программу составил к.э.н. Амелин С.В.
Рабочая программа обсуждена на заседании кафедры экономики, производственного менеджмента и организации машиностроительного производства
протокол
Зав.кафедрой О.Г.Туровец
Одобрена советом
(методической комиссией)
инженерно-экономического факультета
"___"______________2006 г.
Председатель _____________
НАИМЕНОВАНИЕ ТЕМ ИЗУЧАЕМОГО КУРСА
И ИХ СОДЕРЖАНИЕ
ТЕМА 1. Основы линейного программирования
Математические методы в экономике. Примеры экономических задач, решаемых методами математического программирования. Общая, каноническая и стандартная задачи линейного программирования. Геометрическая интерпретация задач линейного программирования. План, опорный план, оптимальный план.
Оптимальное планирование на промышленном предприятии. Модели эффективного использования материальных ресурсов: модель оптимальной загрузки оборудования, модели оптимального раскроя и составления смеси. Моделирование процессов распределения.
ТЕМА 2. Методы решения задач линейного программирования
Симплекс-метод (идея метода, критерий оптимальности опорного плана, переход от одного опорного плана к другому).
ТЕМА 3. Основы теории двойственности
Прямая и двойственная задачи, связь между решениями прямой и двойственной задач. Теорема двойственности. Экономическая интерпретация двойственной задачи.
ТЕМА 4. Транспортная задача
Постановка задачи. Нахождение первоначального опорного плана (метод северо-западного угла, метод минимального элемента). Циклы пересчета. Распределительный метод. Метод потенциалов. Экономические задачи, сводимые к транспортным.
ТЕМА 5. Игровые модели в экономике
Конфликтные ситуации. Игра лиц с нулевой суммой. Платежная матрица, стратегии игроков чистые и смешанные. Седловая точка. Оптимальные максиминные и минимаксные стратегии. Решение игры в смешанных стратегиях. Сведение игровых моделей к моделям линейного программирования. Аналитическое и геометрическое решение игр 2 x 2, 2 x n, m x 2. Элементы теории статистических игр.
Критерии Байеса, Лапласа, Вальда, Сэвиджа, Гурвица, максимакса.
ТЕМА 6. Элементы теории массового обслуживания
Процесс производства как процесс обслуживания. Типы производственных задач, решаемых методами теории массового обслуживания. Поток требований, основные типы потоков. Простейший поток требований, его основные свойства. Основные типы систем массового обслуживания. Характеристика их деятельности. Формулы Эрланга для определения показателей качества функционирования систем массового обслуживания, выбор оптимальной системы.
ТЕМА 7. Сетевые модели и методы планирования и управления
Назначение и область применения. Основные элементы сетевой модели (работа, событие, путь). Принципы и правила построения сетевых графиков. Линейная диаграмма сетевого графика. Расчет основных временных параметров. Оптимизация сетевого графика. Сетевое планирование в условиях неопределенности.
ТЕМА 8. Модели управления запасами
Проблемы оптимизации материальных запасов. Системы регулирования запасов. Типы моделей управления запасами. Задача об экономичной партии с учетом убытков из-за неудовлетворенного спроса. Задача управления запасами с учетом затрат на хранение.
ТЕМА 9. Матричные модели в экономике. Балансовый метод
Принципиальная схема, содержание разделов, основные балансовые соотношения межотраслевого баланса. Модель Леонтьева. Расчет полных, прямых и косвенных затрат. Расчет векторов валового выпуска, конечного продукта и добавленной стоимости. Учет внешнего ресурса в межотраслевом балансе.
Самостоятельная индивидуальная работа должна содержать письменные ответы на теоретические вопросы и решение всех задач по всем перечисленным темам. При выполнении расчетных заданий необходимо привести постановку задачи, расчетные формулы, исходные данные (вариант выбирается по последней цифре в номере зачетной книжки), все промежуточные расчеты и анализ полученных результатов с выводами.
Задания для выполнения самостоятельной работы
Вопросы для письменных ответов:
1. В решении каких производственно-экономических проблем используются методы линейного программирования
2. На чем основан графический метод решения задач линейного программирования (ЛП)
3. Каким образом осуществляется графическая интерпретация системы ограничений задачи ЛП. Как определить область допустимых значений
4. Каким образом строят графическую интерпретацию функции цели и находят максимум и минимум функции цели в задаче ЛП
5. В каком случае задача имеет множество решений (привести графический пример)
6. В каком случае задача не имеет решения (привести графический пример)
7. В каком случае экстремум функции цели находится в бесконечности (привести графический пример)
8. Как определить точные координаты точки оптимума при графическом решении задачи ЛП
Литература: /1, с.19-28; 3, с.82-89; 4, с.55-62/
9. Как построить первоначальный опорный план задачи ЛП в симплексном методе и проверить его оптимальность
10. Как определить переменную (вектор) для включения в базис и переменную (вектор) подлежащую исключению из базиса
11. Какой метод решения систем линейных уравнений лежит в основе симплекс-метода
12. Какой элемент называется разрешающим (ключевым) и какова его роль в пересчете симплексных таблиц
13. Опишите алгоритм симплекс-метода
Литература: /1, с.31-49; 4, с. 63-82; 7, с.21-47/
14. Опишите правила построения двойственной задачи ЛП
15. Какова экономическая интерпретация двойственных оценок
16. Каким образом определяются двойственные оценки из последней симплексной таблицы
17. Сформулируйте задачу оптимального планирования производства и запишите ее в виде модели ЛП
18. Сформулируйте задачу оптимального состава смеси и запишите ее в виде модели ЛП
19. Сформулируйте транспортную задачу ЛП и запишите ее модель
20. Какие существуют методы построения первоначального опорного плана и методы отыскания оптимального решения в транспортной задаче
21. Какие модели транспортной задачи называются открытыми и как преобразовать открытую модель в закрытую
Литература: /1, с.128-171; 2, с.52-64; 3, с.117-138; 4, с.132-184; 7, с.89-102/
Решение задач линейного программирования симплекс-методом
Задание
Допустим предприятие выпускает три вида изделий (И1, И2, И3), используя три вида ресурсов (Р1, Р2, Р3). Запасы ресурсов (З) ограничены. Прибыль от реализации (П) единицы изделия и нормы расхода ресурсов представлены в таблицах. Определить ассортимент и объемы выпуска продукции, получаемую прибыль, величину остатков ресурсов. Найти решение задачи симплексным методом с представлением всех симплексных таблиц (промежуточных шагов решения) и проанализировать полученные результаты. Составить двойственную задачу. Определить двойственные оценки из последней симплексной таблицы и провести анализ последней симплексной таблицы /9/.
 Вариант 1 Вариант 2
Вариант 1 Вариант 2
| И1 | И2 | И3 | З | И1 | И2 | И3 | З | |||
| Р1 | Р1 | |||||||||
| Р2 | Р2 | |||||||||
| Р3 | Р3 | |||||||||
| П | П |
 Вариант 3 Вариант 4
Вариант 3 Вариант 4
| И1 | И2 | И3 | З | И1 | И2 | И3 | З | |||
| Р1 | Р1 | |||||||||
| Р2 | Р2 | |||||||||
| Р3 | Р3 | |||||||||
| П |  | П |
Вариант 5 Вариант 6
| И1 | И2 | И3 | З | И1 | И2 | И3 | З | |||
| Р1 | Р1 | |||||||||
| Р2 | Р2 | |||||||||
| Р3 | Р3 | |||||||||
| П | П |
 Вариант 7 Вариант 8
Вариант 7 Вариант 8
| И1 | И2 | И3 | З | И1 | И2 | И3 | З | |||
| Р1 | Р1 | |||||||||
| Р2 | Р2 | |||||||||
| Р3 | Р3 | |||||||||
| П | П |
 Вариант 9 Вариант 10
Вариант 9 Вариант 10
| И1 | И2 | И3 | З | И1 | И2 | И3 | З | |||
| Р1 | Р1 | |||||||||
| Р2 | Р2 | |||||||||
| Р3 | Р3 | |||||||||
| П | П |
Линейное программирование
решить задачу графическим и аналитическим методами. Для всех вариантов Х1 и Х2 принимают неотрицательные значения
Вариант 1
3Х1 + 3Х2 <= 57 – 15X1 + 2X2 <= 0
– 12X1 + 15X2 <= 60 3X1 + 3X2 >= 57
7X2 <= 77 4X2 >= 44
18X1 – 10X2 <= 90 – 12X1 + 15X2 >=60
f(X) = 4X1 – 6X2 -> max f(X) = 4X1 + 5X2 -> min
Вариант 2
Х1 >= 5 2X1 + X2 <= 10
4X1 + 12X2 <= 252 2X1 + 4X2 <= 8
4X1 + 4X2 <= 120 – 2X1 + 3X2 <= 6
12X1 + 4X2 <= 300 X1 – 8X2 >= 0
f(X) = 10X1 + 10X2 -> max f(X) = – 2X1 – 7X2 -> min
Вариант 3
17Х1 + 12Х2 <= 204 7X1 + 7X2 >= 63
5X2 >= 55 – 12X1 + 15X2 >=60
– 15X1 + 2X2 >= 0 3X1 + 3X2 <= 57
3X1 + 3X2 <= 63 18X1 – 10X2 <= 90
f(X) = – 15X1 – 5X2 -> min f(X) = 7X1 + 15X2 -> max
Вариант 4
Х1 + 4,5Х2 >= 90 X2 <= 70
6X1 + 5X2 <= 300 5X1 + 4X2 <= 200
10X1 + 3X2 <= 300 9X1 – X2 <= 0
4X1 + 3X2 <= 240 5X1 – 4X2 <= 200
f(X) = 3X1 + 2X2 -> max f(X) = – 3X1 – X2 -> min
Вариант 5
3Х1 + 3Х2 >= 57 2X1 >= 34
– 12X1 + 15X2 <= 60 17X1 + 12X2 <= 204
23X1 + 27X2 <= 621 – 10X1 + 25X2 <= 0
18X1 – 10X2 <= 90 23X1 + 27X2 >= 621
f(X) = – 5X1 + 2X2 -> max f(X) = 12X1 + 4X2 -> min
Вариант 6
5Х1 – 4X2 >= 200 4X1 + 3X2 <= 240
9X1 – X2 >= 0 X1 + 0,3X2 <= 30
5X1 + 4X2 >= 200 6X1 + 5X2 <= 300
X2 <= 70 2X1 + 9X2 >= 180
f(X) = 2X1 – 3X2 -> min f(X) = 3X1 + 2X2 -> max
Вариант 7
7Х1 + 7Х2 >= 63 17X1 + 12X2 <= 204
– 12X1 + 15X2 <= 60 11X2 >= 121
17X1 + 12X2 <= 204 – 15X1 + 2X2 <= 0
18X1 – 10X2 <= 90 3X1 + 3X2 >= 57
f(X) = 4X1 + 17X2 -> min f(X) = 2X1 + 15X2 -> max
Вариант 8
18X1 – 10X2 <= 90 5X1 + 4X2 >= 200
– 10X1 + 25X2 <= 0 X2 >= 70
7X1 + 7X2 <= 63 9X1 – X2 >= 0
17X1 + 12X2 <= 204 5X1 – 4X2 >= 200
f(X) = -5X1 – 4X2 -> min f(X) = – 3X1 – 2X2 -> max
Вариант 9
3Х1 + 3Х2 <= 57 – 12X1 + 15X2 >= 60
23Х1 + 27Х2 <= 621 18X1 – 10X2 >= 90
– 15X1 + 2X2 >= 0 23X1 + 27X2 >= 621
5X2 >= 55 10X2 >= 110
f(X) = 3X1 – 4X2 -> max f(X) = 6X1 + 2X2 -> min
Вариант 10
3Х1 + 12Х2 <= 255 X1 + 0,8X2 >= 40
10X1 >= 50 9X1 – X2 >= 0
12X1 + 4X2 <= 300 X2 >= 70
4X1 + 4X2 >= 120 1,25X1 – X2 <= 50
f(X) = 40X1 + 30X2 -> max f(X) = 3X1 + 2X2 -> min
Транспортная задача
Решить задачу распределительным методом или методом потенциалов.
Допустим имеется три поставщика продукции с соответствующими предложениями а1, а2 и а3 и три потребителя, спрос которых составляет в1, в2 и в3 соответственно. Стоимость перевозки единицы груза из каждого пункта отправления до каждого пункта назначения задается матрицей С.
Вариант 1 Вариант 2
а1 = 90, а2 = 40, а3 = 70 а1 = 180, а2 = 80, а3 = 140
в1 = 50, в2 = 50, в3 = 68 в1 = 100, в2 = 100, в3 = 136

 3 4 2 6 3 1
3 4 2 6 3 1
С = 5 6 1 С = 2 4 1
8 3 5 1 3 5
Вариант 3 Вариант 4
а1 = 80, а2 = 70, а3 = 50 а1 = 90, а2 = 40, а3 = 70
в1 = 45, в2 = 27, в3 = 88 в1 = 85, в2 = 37, в3 = 40

 6 4 3 5 2 1
6 4 3 5 2 1
С = 1 5 2 С = 2 4 3
3 1 5 1 3 4
Вариант 5 Вариант 6
а1 = 140, а2 = 120, а3 = 140 а1 = 160, а2 = 140, а3 = 100
в1 = 98, в2 = 122, в3 = 100 в1 = 90, в2 = 54, в3 = 176

 4 2 3 7 2 3
4 2 3 7 2 3
С = 5 3 2 С = 2 5 3
1 2 3 2 1 2
Вариант 7 Вариант 8
а1 = 270, а2 = 120, а3 = 210 а1 = 112, а2 = 238, а3 = 250
в1 = 255, в2 = 111, в3 = 120 в1 = 120, в2 = 130, в3 = 200

 5 2 1 6 2 4
5 2 1 6 2 4
С = 2 4 3 С = 1 5 3
1 3 4 2 2 4
Вариант 9 Вариант 10
а1 = 300, а2 = 100, а3 = 190 а1 = 160, а2 = 155, а3 = 85
 в1 = 213, в2 = 157, в3 = 130 в1 = 115, в2 = 85, в3 = 130
в1 = 213, в2 = 157, в3 = 130 в1 = 115, в2 = 85, в3 = 130
 5 3 2 6 2 3
5 3 2 6 2 3
С = 3 4 1 С = 1 7 3
1 2 1 2 3 4
Модели сетевого планирования и управления
Литература для самостоятельной подготовки
[2,с.178-193], [3,с.142-181], [6,с.309-333], [7,с.145-158]
Вопросы для письменных ответов
1.Каковы цели применения методов СПУ? Охарактеризуйте область применения сетевых методов в сфере экономики.
2.Что представляет собой сетевой график?
3.Что понимается под терминами работа и события, какие разновидности работ Вы знаете?
4.Опишите основные требования, которым должен удовлетворять сетевой график.
5.Как определяются временные оценки работ и событий?
6.Раскройте содержание, метод определения и значение критического пути в моделях сетевого планирования.
7.Как обеспечивается правильная нумерация событий?
Модели сетевого планирования и управления комплексом работ.
Построить сетевую модель выполнения комплекса работ и рассчитать основные временные параметры для всех событий и работ /9/.
Варианты для индивидуального выполнения
Вариант 1 Вариант 2
коды to tнв tп коды to tнв tп
работ работ
1-2 1 2 3 1-2 2 3 4
1-4 1 3 4 1-4 2 4 5
1-6 1 2 4 1-6 2 3 5
2-3 2 3 4 2-3 1 2 3
2-6 2 5 7 2-6 5 8 10
3-5 3 4 5 3-5 6 7 12
4-6 0 0 0 4-6 0 0 0
5-6 0 0 0 5-6 0 0 0
6-7 2 7 9 6-7 5 6 7
7-8 3 9 12 6-8 0 0 0
7-9 2 3 5 7-9 5 7 9
8-11 0 0 0 7-10 5 6 9
8-12 1 2 3 8-11 5 8 9
9-10 2 3 4 9-10 1 2 5
9-11 0 0 0 9-11 1 3 5
10-12 0 0 0 9-12 1 4 5
11-12 4 5 8 10-13 0 0 0
12-13 4 7 8 11-12 0 0 0
11-13 2 3 5
12-13 2 4 5
Вариант 3 Вариант 4
коды to tнв tп коды to tнв tп
работ работ
1-2 3 4 5 1-2 2 3 5
1-4 3 5 6 1-3 2 4 5
1-6 3 4 6 1-4 1 2 5
2-3 1 2 3 1-5 1 3 5
2-6 1 3 4 2-5 0 0 0
3-5 1 2 4 3-6 1 4 5
4-6 0 0 0 4-5 2 4 5
5-6 0 0 0 5-6 3 4 5
6-7 2 3 5 6-7 4 5 6
7-8 2 4 5 7-8 4 5 7
7-9 2 5 7 7-9 4 6 7
7-10 2 6 7 8-9 0 0 0
7-11 2 4 7 8-11 2 3 4
8-11 1 2 3 9-10 2 3 6
9-12 1 3 5 9-12 2 4 6
10-11 0 0 0 10-12 0 0 0
11-12 1 5 7 11-12 0 0 0
12-13 1 7 9 12-13 1 2 3
Вариант 5 Вариант 6
коды to tнв tп коды to tнв tп
работ работ
1-2 2 3 4 1-2 1 2 3
1-4 3 4 5 2-3 2 3 5
1-6 4 5 7 2-5 3 5 7
2-3 1 3 4 2-7 5 7 10
2-6 1 2 4 3-4 7 10 11
3-5 1 5 9 3-7 2 5 7
4-6 0 0 0 4-6 2 7 8
5-6 0 0 0 5-7 0 0 0
6-7 2 3 4 6-7 0 0 0
6-8 4 5 6 7-8 1 2 3
7-8 0 0 0 8-9 1 3 4
8-9 5 6 7 8-10 2 3 4
8-10 6 7 8 8-11 2 4 5
8-11 6 7 10 9-12 2 5 7
8-12 6 8 10 9-13 1 3 5
9-12 0 0 0 10-13 1 5 7
10-13 2 3 4 11-13 3 4 5
11-12 2 4 5 12-13 4 5 6
12-13 2 3 5
Вариант 7 Вариант 8
коды to tнв tп коды to tнв tп
работ работ
1-2 3 4 5 1-2 1 5 7
1-4 4 5 6 1-3 1 2 3
1-6 5 6 7 1-5 2 3 7
2-3 6 7 9 2-3 0 0 0
2-6 1 3 5 2-4 3 4 7
3-5 2 5 7 3-4 3 5 7
4-6 0 0 0 3-6 1 2 5
5-6 0 0 0 4-6 1 3 6
6-7 2 3 4 5-6 1 2 3
6-8 4 5 6 6-7 2 3 4
7-10 4 6 8 7-8 4 5 6
7-11 0 0 0 7-9 6 7 8
8-9 4 8 9 8-10 0 0 0
8-11 1 3 5 8-12 2 3 4
9-12 0 0 0 9-10 4 5 7
10-12 0 0 0 9-11 0 0 0
11-12 3 5 6 10-11 0 0 0
12-13 3 4 6 10-12 1 2 4
11-13 1 3 4
12-13 2 3 4
Вариант 9 Вариант 10
коды to tнв tп коды to tнв tп
работ работ
1-2 0 0 0 1-2 12 14 16
1-3 1 3 5 2-3 6 8 10
1-4 3 4 5 2-3 6 8 10
2-6 1 2 4 2-4 7 8 10
3-5 1 3 4 2-5 10 12 15
3-8 1 4 6 2-6 18 19 21
4-6 8 9 10 3-5 0 0 0
5-6 1 3 6 4-6 0 0 0
6-7 0 0 0 5-7 5 6 8
6-8 1 2 3 6-7 8 9 10
7-9 1 2 4 7-8 4 5 8
7-10 1 3 4 8-9 3 4 8
7-12 1 3 5 8-10 4 5 6
8-12 0 0 0 8-11 5 6 7
9-12 0 0 0 8-12 6 7 8
10-11 5 6 8 9-12 0 0 0
10-12 1 2 3 10-12 0 0 0
11-12 1 3 5 11-12 0 0 0
12-13 7 8 10
Отчет по самостоятельной работе должен содержать:
1. Постановку задачи распределения комплекса работ по календарным плановым периодам и по исполнителям.
2. Исходные данные для построения модели и для расчета сетевого графика.
3. Сетевую модель в графическом исполнении и масштабный сетевой график
(линейную диаграмму).
4. Расчет основных параметров сетевой модели для
работ и событий.
5. Анализ рациональности построенной модели.
Решение экономических задач с помощью
"Теории массового обслуживания"
Литература для самостоятельной подготовки
[2,с.195-208], [7,с.139-145]
Вопросы для письменных ответов
1.Какие системы исследуются при помощи теории массового обслуживания?
2.Привидите примеры систем массового обслуживания в экономике, на производстве.
3.Как классифицируются системы массового обслуживания?
4.Какими чертами обладает простейший поток?
5.Какое распределение обычно имеет время обслуживания?
6.Какое практическое применение имеет теория массового обслуживания при анализе функционирования подразделений производства?
7.Какие важнейшие характеристики функционирования подразделений
производства можно вычислить на основе теории массового обслуживания?
Провести расчеты показателей качества системы массового обслуживания и проанализировать полученные результаты сравнивая их с представленным примером. Пояснить какая система является более приемлемой для внедрения на производстве и почему.
Допустим имеется возможность выбора способа реализации производственного процесса, используя различные технологии и различное оборудование: 1-й способ, рассмотренный в варианте, 2-й способ, для которого необходимо также рассчитать все приведенные показатели и сравнить с 1-м, определяется следующим образом: количество работников необходимо увеличить на 1 для всех вариантов. Интенсивность поступления заявок во всех случаях равна 1 (один из станков выходит из строя в среднем 1 раз в час), время обслуживания станка 6 мин.
| Вариант | ||||||||||
| Кол-во станков | ||||||||||
| Кол-во работников |
Отчет по контрольной работе должен содержать:
1. Постановку задачи теории массового обслуживания.
2. Исходные данные для построения математической модели.
3. Обоснование выбора формул Эрланга.
4. Расчеты основных характеристик модели массового обслуживания (вероятности всех состояний системы и все математические ожидания и коэффициенты простоя).
5. Сравнительный анализ рациональности построенной модели.
Анализ хозяйственных связей с помощью моделей
межотраслевого баланса.
Матричные модели в экономике.Балансовый метод.
[2,с.32-50], [3,с.39-68], [6,с.9-100]
Вопросы для письменных ответов
1.Область применения межотраслевых и межпродуктовых балансов.
2.Что показывает и отражают балансовые модели?
3.Дайте характеристику разделов балансовой модели.
4.Каково различие между промежуточной и конечной продукцией в матричных моделях?
5.Дайте характеристику методов формирования коэффициентов прямых затрат в балансовых моделях.
6.Раскройте экономическое содержание коэффициентов прямых и полных затрат. Как вычисляются эти коэффициенты?
7.Как отражаются в балансовой модели экспорт и импорт продукции?
Задание для индивидуального расчета:
По заданным коэффициентам прямых затрат (матрица А) и заданным значениям конечного продукта для 4-х отраслей (вектор У), найти добавленную стоимость для каждой из четырех отраслей. Представить все промежуточные расчеты.


 . Вар1 Вар2 Вар3
. Вар1 Вар2 Вар3
0.04 0.2 0.3 0.1 0 0.2 0.4 0.3 0.2 0.2 0.3 0.04
А= 0.3 0.2 0.04 0.2 A= 0.1 0.1 0.2 0.05 A= 0.3 0.1 0.04 0.3
0.2 0.3 0.1 0.3 0.2 0.3 0 0.2 0.2 0.3 0.2 0.1
0.1 0.1 0.2 0.3 0.4 0.1 0.3 0 0.1 0.1 0.1 0.2

 Вар4 Вар5 Вар6
Вар4 Вар5 Вар6
0 0.2 0.3 0.2 0.3 0.3 0.2 0.04 0 0.2 0.4 0.3
A= 0.2 0.1 0.2 0.05 A= 0.2 0.1 0.1 0.3 A= 0.1 0.1 0.2 0.05
0.05 0.1 0 0.3 0.1 0.2 0.3 0.1 0.2 0.3 0 0.2
0.3 0.3 0.04 0 0.2 0.1 0.1 0.2 0.4 0.1 0.3 0


 Вар7 Вар 8 Вар9
Вар7 Вар 8 Вар9
0.3 0.1 0.3 0.4 0 0.2 0.1 0.4 0.1 0.1 0.2 0.3
A= 0.4 0.3 0.2 0.3 A= 0.3 0 0.3 0.2 A= 0.2 0.3 0.1 0.4
0.2 0.1 0.2 0.1 0.2 0.5 0.1 0.1 0.3 0.2 0.4 0.2
0.1 0.2 0.1 0.2 0.4 0.3 0.2 0 0.4 0.2 0.3 0.1
 Вар 10
Вар 10
0 0.3 0.2 0.1
A= 0.4 0 0.1 0.2
0.2 0.2 0.3 0.4
0.3 0.1 0.1 0




 Вар1 Вар2 Вар3 Вар4 Вар5 Вар6
Вар1 Вар2 Вар3 Вар4 Вар5 Вар6
 56 29 150 48 27 26
56 29 150 48 27 26
Y= 20 Y= 65 Y= 26 Y= 16 Y= 30 Y= 70
120 100 75 95 116 44
74 32 17 105 96 115



 Вар7 Вар 8 Вар9 Вар 10
Вар7 Вар 8 Вар9 Вар 10
67 90 73 27
Y= 18 Y= 111 Y= 42 Y= 59
35 22 19 117
100 58 110 80
Отчет по самостоятельной работе должен содержать:
1. Постановку задачи межотраслевого баланса.
2. Исходные данные для построения математической модели.
3. Расчетные формулы.
4. Расчеты необходимых характеристик модели.
Игровые модели в экономике
Литература для письменных ответов
[4,с.331-348], [5,с.169-185], [7,с.122-138]
1.Какие причины вызывают неопределенность результатов игры?
2.Как определить нижнюю и верхнюю цену матричной игры и какое соотношение существует между ними?
3.Сформулируйте основную теорему теории матричных игр.
4.Какие существуют методы упрощения игр?
5.Геометрические методы решения игр с матрицами 2хn и mх2 и их применение.
6.На чем основана связь матричной игры и задачи линейного программирования?
7.В чем состоит отличие игры с природой?
8.Перечислите основные критерии решения игр с природой и каковы расчетные формулы для этих критериев.
Найти решение игровых ситуаций графически, аналитически и представить игру в виде задачи линейного программирования /9/.
Допустим в матричной игре два игрока имеют возможность выбора из нескольких вариантов решений. Аi (i=1-m) – стратегии игрока А, Вj (j=1-n) – стратегии игрока В. Значения выигрышей представлены в матрицах по вариантам.



 1) 2) 3) 4) 5)
1) 2) 3) 4) 5)
6 10 0 10 5 6 10 6 12 9
7 9 4 5 1 7 4 15 3 18
8 2 6 1 12 2 11 1 9 13
1 12 2 8 10 4 8 10 14 4
6) 7) 8) 9) 10)



 7 8 6 1 2 5 0 15 1 12
7 8 6 1 2 5 0 15 1 12
10 2 3 6 6 4 5 9 6 8
9 6 1 8 7 6 9 6 10 6
1 11 5 3 8 1 14 4 15 5
Отчет по самостоятельной работе должен содержать.
1. Постановку задачи. Экономико-математическую модель решения игры аналитически и путем приведения игры к задаче линейного программирования.
2. Исходные данные для расчета игровой ситуации.
3. Аналитическое, графическое решение игры и решение игры симплекс-методом.
4.Анализ полученных результатов и выводы по работе.
Теория игр и статистических решений
Определить наилучшую стратегию поведения на рынке товаров и услуг с помощью критериев: Байеса, Лапласа, Вальда, Сэвиджа, Гурвица и максимакса. Сi (i=1-m) – стратегии лица, принимающего решения, Пj (j=1-n) – вероятные состояния рыночной среды, qj – вероятности проявления каждой из n вожможных ситуаций во внешней среде.
Вариант 1
| q1=0,15 | q2=0,2 | q3=0,35 | q4=0,25 | q5=0,05 | |
| П1 | П2 | П3 | П4 | П5 | |
| С1 | |||||
| С2 | |||||
| С3 | |||||
| С4 | |||||
| С5 |
Коэффициент “пессимизма” равен 0,4
Вариант 2
| q1=0,15 | q2=0,2 | q3=0,35 | q4=0,25 | q5=0,05 | |
| П1 | П2 | П3 | П4 | П5 | |
| С1 | |||||
| С2 | |||||
| С3 | |||||
| С4 | |||||
| С5 |
Коэффициент “пессимизма” равен 0,3
Вариант 3
| q1=0,15 | q2=0,2 | q3=0,35 | q4=0,25 | q5=0,05 | |
| П1 | П2 | П3 | П4 | П5 | |
| С1 | |||||
| С2 | |||||
| С3 | |||||
| С4 | |||||
| С5 |
Коэффициент “пессимизма” равен 0,4
Вариант 4
| q1=0,15 | q2=0,2 | q3=0,35 | q4=0,25 | q5=0,05 | |
| П1 | П2 | П3 | П4 | П5 | |
| С1 | |||||
| С2 | |||||
| С3 | |||||
| С4 | |||||
| С5 |
Коэффициент “пессимизма” равен 0,3
Вариант 5
| q1=0,15 | q2=0,2 | q3=0,35 | q4=0,25 | q5=0,05 | |
| П1 | П2 | П3 | П4 | П5 | |
| С1 | |||||
| С2 | |||||
| С3 | |||||
| С4 | |||||
| С5 |
Коэффициент “пессимизма” равен 0,4
Вариант 6
| q1=0,15 | q2=0,2 | q3=0,35 | q4=0,25 | q5=0,05 | |
| П1 | П2 | П3 | П4 | П5 | |
| С1 | |||||
| С2 | |||||
| С3 | |||||
| С4 | |||||
| С5 |
Коэффициент “пессимизма” равен 0,3
Вариант 7
| q1=0,15 | q2=0,2 | q3=0,35 | q4=0,25 | q5=0,05 | |
| П1 | П2 | П3 | П4 | П5 | |
| С1 | |||||
| С2 | |||||
| С3 | |||||
| С4 | |||||
| С5 |
Коэффициент “пессимизма” равен 0,4
Вариант 8
| q1=0,15 | q2=0,2 | q3=0,35 | q4=0,25 | q5=0,05 | |
| П1 | П2 | П3 | П4 | П5 | |
| С1 | |||||
| С2 | |||||
| С3 | |||||
| С4 | |||||
| С5 |
Коэффициент “пессимизма” равен 0,3
Вариант 9
| q1=0,15 | q2=0,2 | q3=0,35 | q4=0,25 | q5=0,05 | |
| П1 | П2 | П3 | П4 | П5 | |
| С1 | |||||
| С2 | |||||
| С3 | |||||
| С4 | |||||
| С5 |
Коэффициент “пессимизма” равен 0,4
Вариант 10
| q1=0,15 | q2=0,2 | q3=0,35 | q4=0,25 | q5=0,05 | |
| П1 | П2 | П3 | П4 | П5 | |
| С1 | |||||
| С2 | |||||
| С3 | |||||
| С4 | |||||
| С5 |
Коэффициент “пессимизма” равен 0,3
ИГРОВЫЕ МОДЕЛИ В ЭКОНОМИКЕ
Конфликтные ситуации. Игра лиц с нулевой суммой. Платежная матрица, стратегии игроков чистые и смешанные. Седловая точка. Оптимальные максиминные и минимаксные стратегии. Решение игры в смешанных стратегиях. Сведение игровых моделей к моделям линейного программирования. Аналитическое и геометрическое решение игр 2х2, 2хn, mх2. Элементы теории статистических игр. Критерии Байеса, Лапласа, Вальда, Сэвиджа, Гурвица, максимакса.
Литература для самостоятельной подготовки
/4,с.331-348/, /5,с.169-185/, /7,с.122-138/
1.Какие причины вызывают неопределенность результатов игры?
2.Как определить нижнюю и верхнюю цену матричной игры и какое соотношение существует между ними?
3.Сформулируйте основную теорему теории матричных игр.
4.Какие существуют методы упрощения игр?
5.Геометрические методы решения игр с матрицами 2хn и mх2 и их применение.
6.На чем основана связь матричной игры и задачи линейного программирования?
7.В чем состоит отличие игры с природой?
8.Перечислите основные критерии решения игр с природой и каковы расчетные формулы для этих критериев.
Допустим, игра задана матрицей В1 В2
А1 0 5
А2 1 3
А3 3 2
Решим игру графически, аналитически и путем приведения к задаче линейного программирования.
Если при вычислении максиминной стратегии для игрока А (нижней цены игры) и минимаксной стратегии для его противника (верхней цены игры) не будет найдена седловая точка, то такая игра имеет решение в смешанных стратегиях. Для этого необходимо решить систему трех уравнений, предварительно представив игру в виде "игры два на два"
Для решения задачи аналитически составим следующие системы уравнений:
0•q1 + 5•q2 = V 0•P1 + 3•P3 = V
3•q1 + 2•q2 = V 5•P1 + 2•P3 = V
q1 + q2 = 1 P1 + P3 = 1,
и используем приведенные соотношения.
Если игра задана матрицей В1 В2
А1 а11 а12
А2 а21 а22, тогда
Р1=(а22 - а21)/(а11 - а12 + а22 - а21)
Р2=(а11 - а12)/(а11 - а12 + а22 - а21)
V=(a11 • a22 - a21 • a12)/(а11 - а12 + а22 - а21)
q1=(a22 - a12)/(а11 - а12 + а22 - а21)
q2=(a11 - a21)/(а11 - а12 + а22 - а21)
Для решения задачи, путем приведения ее к задаче линейного программирования, введем обозначения: Хi = Pi /V; Yj = qj / V; V = 1 / f(x), тогда
0•y1 + 5•y2 = 1 0•x1 + 3•x3 = 1
3•y1 + 2•y2 = 1 5•x1 + 2•x3 = 1
y1 + y2 = 1/V ® max x1 + x3 = 1/V ® min,
Пример для игры “три на три”. Допустим, игрок А имеет три “чистые” стратегии А1, А2, А3, а игрок В – три “чистые” стратегии В1,В2,B3. Игра задана платежной матрицей
| В1 | В2 | В3 | |
| А1 | |||
| А2 | |||
| А3 |
Здесь нижняя цена игры a=3, верхняя цена игры b=10. Для того, чтобы найти оптимальную смешанную стратегию игрока A, нужно решить следующую задачу линейного программирования:
min f(x)=x1+x2+x3
8x1+3x2+10x3³1
3x1+10x2+x3³1
10x1+x2+12x3³1
x1,x2,x3³0
Решая эту задачу симпелекс-методом, находим оптимальный план
x*=(1/24, 1/12, 1/24, 0, 0, 0), max f(x)=1/6.
Поэтому цена игры V=6, а оптимальная смешанная стратегия SA=(¼, ½, ¼).
Решение двойственной задачи можно найти используя теоремы двойственности. Для оптимальных планов х* и y* должно выполняться условие f(x*)=g(y*). Решение двойственной задачи y*=(1/24, 1/12, 1/24), поэтому
SВ=(¼, ½, ¼).
Варианты индивидуальных заданий.




 Вариант 1 Вариант 2 Вариант 3 Вариант 4 Вариант 5
Вариант 1 Вариант 2 Вариант 3 Вариант 4 Вариант 5
6 7 9 11 2 4 7 11 1 6 10 15 0 5 9 14 1 4 6 10
12 8 3 1 12 10 8 7 12 8 6 5 15 9 6 4 11 5 3 2




 2015-04-08
2015-04-08 1016
1016