Задача № 5 выполняется по теме «Ряды динамики».
Ряд динамики – это ряд значений статистического показателя, расположенных в хронологической последовательности, т.е. характеризующих изменения явления во времени. Таким образом, ряд включает два основных элемента: момент или интервал времени, к которому относятся данные, и значение показателя, которые чаще всего называют уровни ряда.
Уровни ряда могут быть выражены абсолютными, относительными или средними величинами.
Динамические ряды могут быть интервальными и моментными.
Изучение динамических рядов предполагает определение показателей интенсивности отдельных изменений уровней и их усреднение, расчет среднего уровня ряда динамики, анализ закономерностей изменения уровней ряда.
Изменение динамического ряда характеризуют с помощью показателей динамики. К ним относятся: абсолютный прирост, коэффициент роста, темп роста, темп прироста, абсолютное значение одного процента прироста.
В зависимости от базы сравнения различают базисные и цепные показатели динамики. Базисные показатели динамики – это результат сравнения текущих уровней с одним фиксированными уровнем, принятым за базу (обычно начальным). Цепные показатели динамики - это результат сравнения текущих уровней с предшествующими. Формулы расчета представлены ниже:
1) Абсолютный прирост
| базисный | цепной |
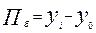
| 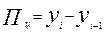
|
2) Коэффициент роста
| базисный | цепной |
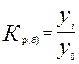
| 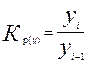
|
3) Темп роста 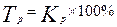 ;
;
4) Темп прироста 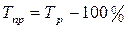 ;
;
5) Абсолютное значение одного процента прироста 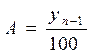 ;
;
6) Средний абсолютный прирост
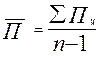 =
= 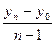 ;
;
7) Средний темп роста
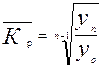 ;
;
8) Средний темп роста 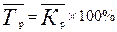
9) Средний темп прироста 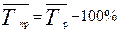 .
.
Метод определения среднего уровня зависит от типа динамического ряда. Средний уровень интервального ряда определяется как средняя арифметическая простая:
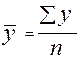 ,
,
где: y – значение соответствующего уровня;
n – число уровней ряда.
Средний уровень моментного ряда определяется:
а) для ряда с разноотстоящими моментами наблюдения – по формуле:
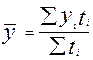 ,
,
где ti – интервал времени между моментами;
Σ ti – общая продолжительность ряда.
б) для ряда с равноотстоящими моментами наблюдения – по формуле средней хронологической:
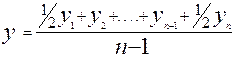
Для выявления закономерностей (тенденции) динамического ряда используют эмпирическое и аналитическое выравнивание.
Среди методов эмпирического выравнивания следует выделить метод укрупнения интервалов (замена дневных данных недельными, недельных – декадными или месячными и т.д.) и метод скользящей средней (последовательное усреднение соседних уровней).
При аналитическом выравнивании эмпирические уровни заменяются теоретическими, рассчитанными на основе математической функции:
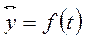 ,
,
где в качестве независимой переменной выступает фактор времени.
Выравнивание ряда сводится к определению параметров функции. Наиболее точный результат позволяет получить метод наименьших квадратов. Часто используется так называемый метод отсчета от условного нуля – все порядковые номера уровней заменяются условными таким образом, чтобы 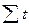 = 0, а шаг между уровнями сохранялся неизменным.
= 0, а шаг между уровнями сохранялся неизменным.
Наиболее простая функция – прямая типа 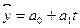 .
.
При выравнивании с помощью линейной функции параметры определяются следующим образом:
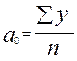 ,
, 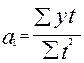 .
.
 2015-04-08
2015-04-08 342
342








