2015-04-08
313
Задача № 4 выполняется по теме «Статистические методы анализа взаимосвязей».
Связь – такое явление, при котором изменение одного признака определяется изменением другого (других) признака. Признаки, испытывающие влияние – эндогенные, внутренние, результаты; признаки, оказывающие влияние – экзогенные, внешние, факторы.
По степени тесноты связи подразделяют на:
1) функциональные (жестко детерминированные) – одному значению фактора соответствует строго определенное значение результата;
2) статистические (стохастические, случайные, корреляционные) – одному и тому же значению признака-фактора могут соответствовать разные значения результативного признака и наоборот. Связь проявляется при большом числе наблюдений в среднем изменении фактора и результата.
По направлению выделяют связь прямую и обратную. По аналитическому выражению обычно выделяют связи прямолинейные (линейные) и криволинейные.
Для оценки тесноты связей применятся ряд показателей, одни из которых называются эмпирическими или непараметрическими, другие – теоретическими.
В задаче № 4 следует рассчитать непараметрические показатели и показатели тесноты связи качественных признаков.
Коэффициент корреляции знаков (коэффициент Фехнера) вычисляется на основании определения знаков отклонений вариантов двух взаимосвязанных признаков от средних величин.
Если число совпадений знаков обозначить через а, число несовпадений - через в, а сам коэффициент – через Ф, то формулу можно написать так:
.
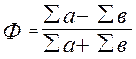Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывается по рангам двух взаимосвязанных признаков следующим образом:
,
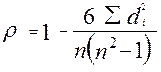где: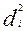 
- квадраты разности рангов;
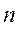- число наблюдений (число пар рангов).
Например, имеется информация о местах, занятыми 10 спортсменами на чемпионате Европы и Олимпийских играх:
| Номер спортсмена | ИТОГО | ||||||||||
| Место (ранг) на чемпионате | - | ||||||||||
| Место (ранг) на играх | - | ||||||||||
| d | -5 | -3 | -2 | ||||||||
| d2 |
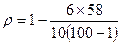= 0,649
Для определения тесноты связи между тремя и более признаками применяется ранговый коэффициент согласия – коэффициент конкордации, который вычисляется по формуле:
,
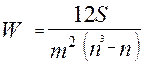где: 
- количество факторов;
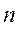- число наблюдений;
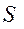- сумма квадратов отклонений рангов.
Например, 8 предприятий ранжированы по уровню рентабельности, уровню качества и уровню спроса на продукцию:
| Номер предприятия | Ранг по | Сумма рангов | Квадрат суммы рангов | ||
| рентабельности | качеству | спросу | |||
| ИТОГО |
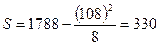
Коэффициент конкордации:
.
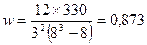Для вычисления коэффициентов ассоциации и контингенции строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным.
| I | II | ||
| а | b | а+b | |
| с | d | с+d | |
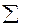
| а+с | b+d |
Коэффициент ассоциации:
.
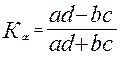Коэффициент контингенции:
.
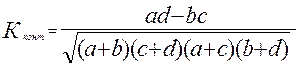Если каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициентов взаимной сопряженности Пирсона и Чупрова. Эти коэффициенты вычисляются по формулам:
,
,
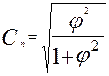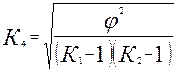где: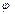 
2 - показатель взаимной сопряженности;
К 1 - число значений (групп) первого признака;
К 2 - число значений (групп) второго признака.
Расчет коэффициента взаимной сопряженности производится по следующей схеме:
| Группы признака А | Группы признака В | Итого | ||
| В 1 | В2 | В 3 | ||
| А1 А2 А3 | f 1 f 4 f 7 | f 2 f 5 f 8 | f 3 f 6 f 9 | n 1 n 2 n 3 |
| m 1 | m 2 | m 3 |
Расчет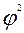 
производится так:
̶ по первой строке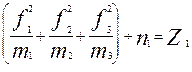 
;
̶ по второй строке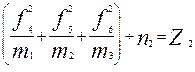 
;
̶ по третьей строке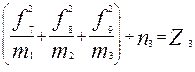 
.
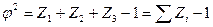
Непараметрические коэффициенты связи могут изменяться от 0 до 1. Чем ближе абсолютные значения к 1, тем теснее связь между исследуемыми признаками.
