Примеры решения задач. Пример 1. Уравнение движения материальной точки вдоль оси имеет вид x=A+Bt+Ct3, где A=2 м, В=1 м/с, С=–0.5 м/с3

Пример 1. Уравнение движения материальной точки вдоль оси имеет вид x=A+Bt+Ct³, где A =2 м, В =1 м/с, С= –0.5 м/с³. Найти координату х, скорость 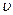_x и ускорение а_x точки в момент времени t =2с.

Решение. Координату х найдем, подставив в уравнение движения числовые значения коэффициентов А, В и С и времени t:

х = (2+1×2 – 0.5 2³) м = 0.

Мгновенная скорость относительно оси х есть первая производная от координаты по времени:

.

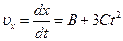Ускорение точки найдем, взяв первую производную от скорости по времени:

.

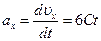В момент времени t = 2с

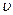_x = (1-3×0,5×2²) м/с= – 5 м/с; а_х = б(— 0,5)×2 м/с²= – 6 м/с².

Пример 2. Тело вращается вокруг неподвижной оси по закону j=А+Вt+Ct², где А=10 рад, В =20 рад/с, С= – 2 рад/с². Найти полное ускорение точки, находя­щейся на расстоянии r =0,1 м от оси вращения, для момента времени t=4 с.

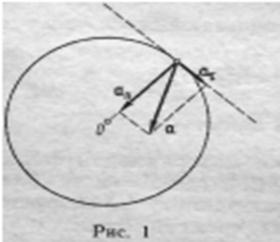Решение. Полное ускорение а точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения а_t, направленного по касательной к траектории, и нормального ускорения a_n, направленного к центру кривизны траектории (рис. 1):

а = a_t +a_n.

Так как векторы а_т и а_n взаимно перпендикулярны, то модуль ускорения

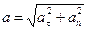– 11 –

. (1)

Модули тангенциального и нормального ускорения точки вращающегося тела выражаются формулами а_t = er, а_n = w²r,

где w – модуль угловой скорости тела; e – модуль его углового ускорения. Подставляя выражения a_t и а_п в формулу (1), находим

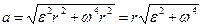. (2)

Угловую скорость w найдем, взяв первую производную угла поворота по времени: .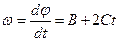

В момент времени t=4c модуль угловой скорости

w=[20 + 2(-2)4] рад/с = 4 рад/с.

Угловое ускорение найдем, взяв первую производную от угловой скорости по времени:

e=dw/dt = 2С = — 4 рад/с².

Подставляя значения w, e и r в формулу (2), получаем

а = 0,1 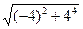м/с²= 1,65 м/с².

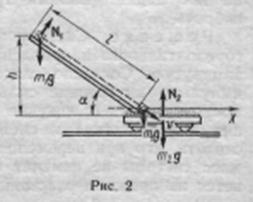Пример 3. Ящик массой т₁ = 20 кг соскальзывает по идеально гладкому лотку длиной l=2 м на неподвижную тележку с песком и застревает в нем. Тележка с песком массой m₂=80 кг может свободно (без трения) перемещаться по рельсам в горизонтальном направлении. Определить скорость и тележки с ящиком, если лоток наклонен под углом a=30° к рельсам.

Решение. Тележку и ящик можно рассматривать как систему двух неупруго взаимодействующих тел.

Но эта система не замкнута, так как на нее действуют внешние силы: силы тяжести m₁g и m₂g и сила реакции N₂ (рис. 2). Поэтому применить закон сохранения импульса к системе ящик – тележка нельзя. Но так как проекции указанных сил на направление оси х, совпадающей с направлением рельсов, равны

нулю, то проекцию импульса системы на это направление можно считать

– 12 –

постоянной, т. е.

Р_1x+ р_2x = p`<sub>1x</sub> + p`_2x, (1),

где р_1x и р_2x – проекции импульса ящика и тележки с песком в момент падения ящика на тележку; p’_1x и p'_2x – те же величины после падения ящика. Рассматривая тела системы как материальные точки, выразим в равенстве (1) импульсы тел через их массы и скорости, учитывая, что р_2x= 0 (тележка до взаимодействия с ящиком покоилась), а также что после взаимодействия оба тела системы движутся с одной и той же скоростью и:

m_{1 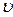1x} = (m₁+ т₂) и, или m_{1 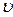1} cosa= (m₁ +m₂) и,

где 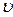₁– модуль скорости ящика перед падением на тележку; 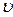_1x = 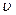₁cosa – проекция этой скорости на ось х.

Отсюда 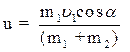(2)

Модуль скорости 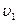определим из закона сохранения энергии:

m₁gh = ½ m₁ 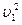, где h =lsina, откуда

= .

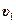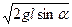Подставив выражение 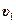в формулу (2), получим

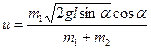
После вычислений найдем

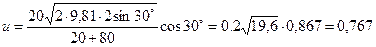м/c.

Пример 4. При выстреле из пружинного пистолета вертикально вверх пуля массой m=20 г поднялась на высоту h=5 м. Определить жесткость k пружины пистолета, если она была сжата на ∆ х=10 см. Массой пружины и силами трения пренебречь.

Решение. Рассмотрим систему пружина – пуля. Так как на тела системы действуют только консервативные силы, то для решения задачи можно применить закон сохранения энергии в механике. Согласно ему полная механическая энергия E системы в начальном состоянии (в данном случае перед выстрелом)

– 13 –

равна полной энергии Е в конечном состоянии (когда пуля поднялась на высоту h), т.е.

Е₁=Е₂, или Т₁+П₁=Т₂+П₂, (1)

где Т₁, Т₂, П₁ и П₂ – кинетические и потенциальные энергии системы в начальном и конечном состояниях.

Так как кинетические энергии пули в начальном и конечном состояниях равны нулю, то равенство (1) примет вид

П₁=П₂. (2)

Примем потенциальную энергию пули в поле сил тяготения Земли, когда пуля покоится на сжатой пружине, равной нулю, а высота подъема пули будет отсчитываться от торца сжатой пружины. Тогда энергия системы в начальном состоянии будет равна потенциальной энергии сжатой пружины, т.е. П₁= ½ k(∆x) ², а в конечном состоянии – потенциальной энергии пули на высоте h, т.е. П₂=mgh.

Подставив выражения П₁ и П₂ в формулу (2), найдем ½ k(∆x)² =mgh, откуда

k=2mgh/x². (3)

Проверим, дает ли полученная формула единицу жесткости k. Для этого в правую часть формулы (3) вместо величин подставим их единицы (единицу какой-либо величины принято обозначать символом этой величины, заключенным в квадратные скобки):

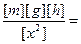(1кг×1м×с^-2×1м)/1м²=(1кг×м×с^-2)/1м=1Н/м.

Убедившись, что полученная единица является единицей жесткости (1Н/м), подставим в формулу (3) значения величин и произведем вычисления:

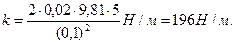
Пример 5. Шар массой m₁, движущийся горизонтально с некоторой скоростью 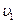, столкнулся с неподвижным шаром массой m₂. Шары абсолютно упругие, удар прямой, центральный. Какую долю e своей кинетической энергии первый шар передал второму?

– 14 –

Решение. Доля энергии, переданной первым шаром второму, выразится соотношением

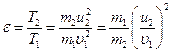(1)

где Т₁ – кинетическая энергия первого шара до удара; u₂ и Т₂ –скорость и кинетическая энергия второго шара после удара.

Как видно из формулы (1), для определения e надо найти u₂. Согласно условию задачи, импульс системы двух шаров относительно горизонтального направления не изменяется и механическая энергия шаров в другие виды не переходит. Пользуясь этим, найдем:

M₁ 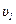=m₁u₁+m₂u₂; (2)

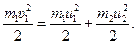(3)

Решив совместно уравнения (2) и (3) найдем :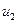

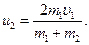
Подставив это выражение u₂ в формулу (1) и сократив на 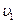и m₁, получим

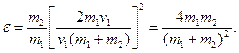
Из найденного соотношения видно, что доля переданной энергии зависит только от масс сталкивающихся шаров.

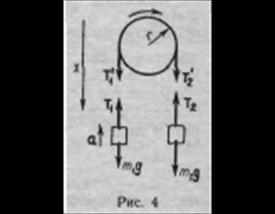Пример 6. Через блок в виде сплошного диска, имеющего массу m=80г (рис. 4), перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами m₁ =100г и m₂ =200г. Определить ускорение, с которым будут двигаться грузы, если их предоставить самим себе. Трением и массой нити пренебречь.

Решение. Рассмотрим силы, действующие на каждый груз и на блок в отдельности. На каждый груз действуют две силы: сила тяжести и сила упругости (сила натяжения нити). Направим ось х вертикально

– 15 –

вниз и напишем для каждого груза уравнение движения (второй закон Ньютона) в проекциях на эту ось. Для первого груза

T₁ - m₁g = m₁a (1)

для второго груза

m₂g - T ₂ = m₂a (2)

Под действием моментов сил T₁ и T₂ относительно оси z, перпендикулярной плоскости чертежа и направленной за чертеж, блок приобретает угловое ускорение e. Согласно основному уравнению динамики вращательного движения,

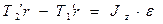, (3)

где 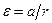; 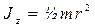– момент инерции блока (сплошного диска) относительно оси z.

Согласно третьему закону Ньютона, с учетом невесомости нити 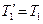, 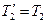. Воспользовавшись этим, подставим в уравнение (3) вместо 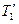и 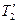выражения Т₁ и Т₂, получив их предварительно из уравнений (1) и (2):

(m₂g-m₂a)r-(m₁g+m₁a)r=mr²a/(2r).

После сокращения на r и перегруппировки членов найдем

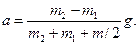(4)

Формула (4) позволяет массы m₁, m₂ и m выразить в граммах, как они даны в условиях задачи, а ускорение – в единицах СИ. После подстановки числовых значений в формулу (4) получим

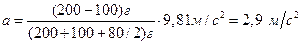
Пример 7. Маховик в виде сплошного диска радиусом R=0,2м и массой m=50 кг раскручен до частоты вращения n₁=480 мин^-1 и предоставлен сам

себе. Под действием сил трения маховик остановился через t=50c. Найти момент М сил трения.

Решение. Для решения задачи воспользуемся основным уравнением динамики вращательного движения в виде

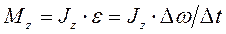(1)

– 16 –

где М_г –момент внешних сил (в данном случае момент сил трения), действующих на маховик относительно оси z, J_z –момент инерции маховика относительно оси z; Dw – изменение угловой скорости маховика за время .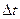

Момент инерции маховика в виде сплошного диска определяется по формуле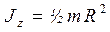

Изменение угловой скорости Dw=w₂-w₁ выразим через конечную n₂ и начальную п₁ частоты вращения, пользуясь соотношением w = 2pn:

Dw=w₂-w₁ =2pn₂-2pn₁=2p(n₂-n₁).

Подставив в формулу (1) выражения J_z и Dw, получим

M_z=pmR²(n₂-n₁)/Dt. (2)

Проверим, дает ли расчетная формула единицу момента силы (Н×м). Для этого в правую часть формулы вместо символов величин подставим их единицы:

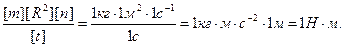
Подставим в (2) числовые значения величин и произведем вычисления, учитывая, что n₁ =480мин^-1=480/60с^-1 = 8с^-1:

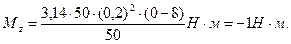
Знак минус показывает, что момент сил трения оказывает на маховик тормозящее действие.

Пример 8. Платформа в виде сплошного диска радиусом R=1,5 м и массой m₁=180 кг вращается около вертикальной оси с частотой n=10 мин^-1. В центре платформы стоит человек массой m₂=60 кг. Какую линейную скорость 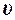относительно пола помещения будет иметь, человек, если он перейдет на край платформы?

Решение. Согласно условию задачи, момент внешних сил относительно оси вращения z, совпадающей с геометрической осью платформы, можно считать равным нулю. При этом условии проекция L_z момента импульса системы платформа – человек остается постоянной:

– 17 –

L_z=J_zw = const, (1)

где J_z – момент инерции платформы с человеком относительно оси z; w – угловая скорость платформы. Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы, поэтому в начальном состоянии J_z=J₁+J₂, а в конечном состоянии .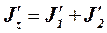

С учетом этого равенство (1) примет вид

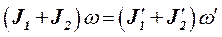(2)

где значения моментов инерции J₁ и J₂ платформы и человека соответственно относятся к начальному состоянию системы; 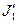и 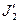– к конечному.

Момент инерции платформы относительно оси z пpи переходе человека не изменяется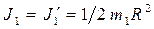

Moмент инерции человека относительно той же оси будет изменяться.

Если рассматривать человека как материальную точку, то его момент инерции J₂ в начальном состоянии (в центре платформы) можно считать равным нулю. В конечном состоянии (на краю платформы) момент инерции человека J₂’=m₂R². Подставим в формулу (2) выражения моментов инерции, начальной угловой скорости вращения платформы с человеком (w = 2pn) и конечной угловой скорости (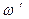 = 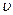/R, где 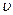– скорость человека относительно пола) ( 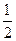m₁R²+0) 2pn = ( 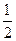m₁R² + m₂R²) 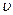/R.

После сокращения на R² и простых преобразований находим скорость:

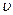= 2pnRm₁ /(m₁+2m₂).

Произведем вычисления:

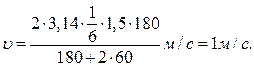
Пример 9. Ракета установлена на поверхности Земли для запуска в

вертикальном направлении. При какой минимальной скорости 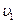, сообщенной ракете при запуске, она удалится от поверхности на расстояние, равное радиусу

– 18 –

Земли (R = 6.37×10⁶ м)? Всеми силами, кроме силы гравитационного взаимодействия ракеты и Земли, пренебречь.

Решение: Со стороны Земли на ракету действует сила тяжести, являющаяся потенциальной силой. При неработающем двигателе под действием потенциальной силы механическая энергия ракеты изменяться не будет. Следовательно.

Т₁ + П₁ = Т₂ + П₂, (1)

где Т₁, П₁ и Т₂, П ₂ – кинетическая и потенциальная энергии ракеты после выключения двигателя в начальном (у поверхности Земли) и конечном (на расстоянии, равном радиусу Земли) состояниях. Согласно условию задачи П₁=0, Т₂=0, T₁= m 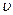² / 2, П₂=mgR. Следовательно, 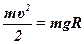и .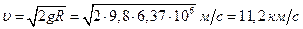

Пример 10. Точка совершает гармонические колебания с частотой v=10Гц. В момент, принятый за начальный, точка имела максимальное смещение: x_max= 1 мм. Написать уравнение колебаний точки и начертить её график.

Решение. Уравнение колебаний точки можно записать в виде

x = Asin(wt + j₁), (1)

где А – амплитуда колебаний; w – циклическая частота, t – время; j₁ – начальная фаза.

По определению, амплитуда колебаний A = x_max. (2)

Циклическая частота w связана с частотой n соотношением

w = 2pn, (3)

Для момента времени t=0 формула (1) примет вид x_max= Asinj₁, откуда начальная фаза

j₁ = arcsin 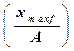= arcsin 1, или j₁=(2k+l)×p/2 (k= 0, 1, 2,...).

Изменение фазы на 2p не изменяет состояния колеблющейся точки, поэтому можно принять j₁ = p/2. (4)

С учетом равенств (2)-(4) уравнение колебаний примет вид

– 19 –

x=Asin(2pnt+p/2), или x = Acos2pnt,

где А=1мм=10^-3м,

График соответствующего гармонического колебания приведен на рис.5.

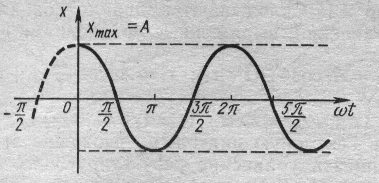
Рис.5

Пример 11. Частица массой т= 0,01 кг совершает гармонические колебания с периодом Т= 2с. Полная энергия колеблющейся частицы

E=0,1мДж. Определить амплитуду А колебаний и наибольшее значение силы F_max, действующей на частицу.

Решение. Для определения амплитуды колебаний воспользуемся выражением полной энергии частицы:

Е = ½ mw²A²,

где w = 2p/Т. Отсюда амплитуда

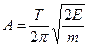(1)

Так как частица совершает гармонические колебания, то сила, действующая на нее, является квазиупругой и, следовательно, может быть выражена соотношением F= – kx, где k – коэффициент квазиупругой силы; х – смещение колеблющейся точки. Максимальной сила будет при максимальном смещении x_max равном амплитуде:

F_max=kA. (2)

Коэффициент k выразим через период колебаний:

k = mw²=m4p² /T². (3)

Подставив выражения (1) и (3) в (2) и произведя упрощения, получим

.

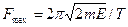– 20 –

Произведем вычисления:

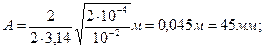
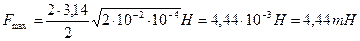
Пример 12. Складываются два колебания одинакового направления, выраженные уравнениями

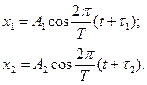
где A₁ = 3см, A₂ =2см, t₁, = 1/6с, t₂=1/3с, T = 2с. Построить векторную диаграмму сложения этих колебаний и написать уравнение результирующего колебания.

Решение. Для построения векторной диаграммы сложения двух колебаний одного направления надо фиксировать какой-либо момент времени. Обычно векторную диаграмму строят для момента времени t = 0. Преобразовав оба уравнения к канонической форме x=Acos(wt+j), получим

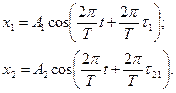
Отсюда видно, что оба складываемых гармонических колебания имеют одинаковую циклическую частоту

w = 2p/T.

Начальные фазы первого и второго колебаний соответственно равны

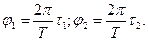
Произведем вычисления:

– 21 –

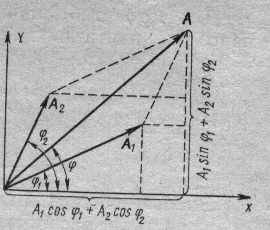
Изобразим векторы a₁ и А₂. Для этого отложим от резки длиной А₁ = 3 см и А₂ = 2 см под углами j₁= 30° в j₂=60° к оси Ох. Результирующее колебание будет происходить с той же частотой w и амплитудой А, равной

геометрической сумме амплитуд a₁ и A₂: A = A₁ +A₂ Согласно теореме косинусов,

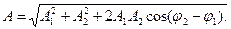
Начальную фазу результирующего колебания можно также определить непосредственно из векторной диаграммы (рис 6):

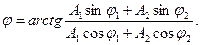
Произведем вычисления:

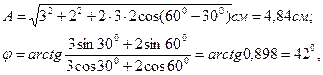
или j=0,735 рад.

Рис.6.

Так как результирующее колебание является гармоническим, имеет ту же частоту, что и слагаемые колебания, то его можно записать в виде

x=Acos(wt+j) где A = 4.84см, w = 3,14 с^-1, j-=0,735рад.

Пример 13. Плоская волна распространяется вдоль прямой со скоростью 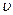= 20 м/с. Две точки, находящиеся на этой прямой на расстояниях x₁=12м и x₂ = 15м от источника волн, колеблются с разностью фаз Dj=0,75p. Найти длину волны l написать уравнение волны и найти смешение указанных точек в момент t=1,2 с, если амплитуда колебаний A = 0,1 м.

Решение: Точки, находящиеся друг от друга на расстоянии, равном длине волны l, колеблются с разностью фаз, равной 2p; точки, находящиеся друг от друга на любом расстоянии Dx, колеблются с разностью фаз, равной

Dj = Dx×2p/l = (x₂-x₁) ×2p/l..

Решая это равенство относительно l, получаем

l=2p(x₂-x₁)/Dj. (1)

– 22 –

Подставив числовые значения величин, входящих в выражение (1), и выполнив арифметические действия, получим

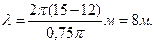
Для того чтобы написать уравнение плоской волны надо еще найти циклическую частоту w. Так как w=2p/T (T=l/ 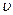– период колебаний), то w=2pv/l.

Произведем вычисления:

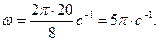
Зная амплитуду А колебаний, циклическую частоту w и скорость v распространения волны, можно написать уравнение плоской волны для данного случая:

y=Acosw(t-x/ 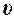), (2)

где А=0,1 м, w=5pс^-1, 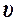=20 м/c.

Чтобы найти смещение y указанных точек, достаточно в уравнение (2) подставить значения t и x.

y₁=0,1cos5p(1,2-12/20)м=0,1cos3p м=-0,1 м;

y₂=0,1cos5p(1,2-15/20)м=0,1cos2,25p м=0,1cos0,25p м=0,071 м=7,1 см.