Коэффициент корреляции рангов (коэффициент СПИРМЕНА)
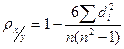 ,
,
где 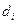 - разность рангов; n – число наблюдений
- разность рангов; n – число наблюдений
ранг – порядковый номер значений признака упорядоченного ряда
КОЭФФИЦИЕНТ ДЕТЕРМИНАЦИИ (D или 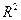 )
)
· этодоля межгрупповой дисперсии в общей дисперсии
· показывает тесноту связи
· 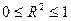
· Чем ближе к 1, тем теснее связь, чем ближе к 0, тем мене тесная (слабее) связь
КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ (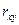 )
)
· Характеризует тесноту и направление ЛИНЕЙНОЙ
· связи между двумя признаками на фоне действия остальных, входящих в модель признаков
· ЧАСТНЫЙ коэффициент корреляции характеризует тесноту и направление линейной связи между двумя признаками исключая действие остальных, входящих в модель, признаков
· 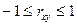 ;
; 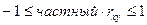
| Направление линейной связи | |
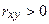
| Связь прямая, т.е. с ростом значений факторной переменной 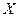 растут средние значения результативной переменной растут средние значения результативной переменной 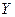
|
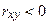
| Связь обратная, т.е. с ростом значений факторной переменной 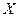 растут средние значения результативной переменной растут средние значения результативной переменной 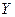 убывают убывают
|
Теснота линейной связи между 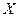 и и 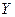
| |
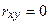
| Линейная связь между 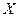 и и 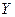 полностью отсутствует полностью отсутствует
|
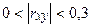
| Линейная связь практически отсутствует |
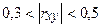
| Связь слабая |
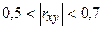
| Связь умеренная |
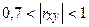
| Сильная связь |
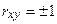
| Связь жестко функциональная. Все эмпирические точки лежат на линии регрессии |
· МНОЖЕСТВЕННЫЙ коэффициент корреляции 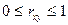
· Чем ближе 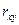 к
к 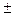 1, тем ТЕСНЕЕ связь, чем ближе к 0, тем связь слабее
1, тем ТЕСНЕЕ связь, чем ближе к 0, тем связь слабее
ЭМПИРИЧЕСКОЕ КОРРЕЛЯЦИОННОЕ ОТНОШЕНИЕ (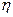 )
) 
· Определяет ТЕСНОТУ связи при НЕЛИНЕЙНОЙ зависимости
· 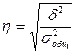
 , где
, где 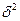 - межгрупповая дисперсия;
- межгрупповая дисперсия; 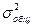 - общая дисперсия
- общая дисперсия
ТЕСНОТА КОРРЕЛЯЦИОННОЙ СВЯЗИ между двумя КОЛИЧЕСТВЕННЫМИ признаками измеряется с помощью
· Коэффициента корреляции знаков (Фехнера)
· Линейного коэффициента корреляции
· Коэффициента корреляции рангов (Спирмена)
· Корреляционное отношение
· Коэффициента детерминации в парной регрессии
ТЕСНОТА СВЯЗИ между двумя АЛЬТЕРНАТИВНЫМИ признаками
· Коэффициент ассоциации
· Коэффициент контингенции
ВИД СВЯЗИ
· Линейная, или прямолинейная: 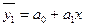
· Нелинейная, например, 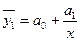

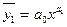
ДЛЯ УРАВНЕНИЯ 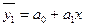
· Коэффициент 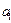 показывает: С РОСТОМ признака Х на 1, признак У возрастает (если
показывает: С РОСТОМ признака Х на 1, признак У возрастает (если 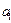 >0) или убывает (если
>0) или убывает (если 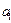 <0) НА
<0) НА 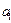 ЕДИНИЦ
ЕДИНИЦ
. Если связь между 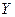 и
и 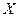 линейна, т.е.
линейна, т.е. 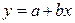 , то применение метода наименьших квадратов дает формулы для расчета коэффициентов
, то применение метода наименьших квадратов дает формулы для расчета коэффициентов 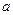 и
и 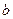 :
:
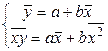 здесь средние величины рассчитываются по формулам
здесь средние величины рассчитываются по формулам
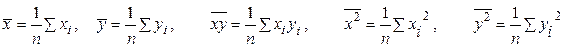
Для оценки регрессионного уровня рассчитывают следующие величины:
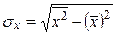 - среднее квадратическое отклонение переменной
- среднее квадратическое отклонение переменной 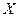 ;
;
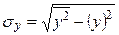 - среднее квадратическое отклонение переменной
- среднее квадратическое отклонение переменной 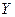 ;
;
Значение функции 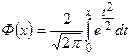 Приложение
Приложение
| Целые и десятые доли t | Сотые доли t | ||||
| 0,0 | 0,0000 | 0,0160 | 0,0319 | 0,0478 | 0,0638 |
| 0,1 | |||||
| 0,2 | |||||
| 0,3 | |||||
| 0,4 | |||||
| 0,5 | |||||
| 0,6 | |||||
| 0,7 | |||||
| 0,8 | |||||
| 0,9 | |||||
| 1,0 | 0,6827 | 0,6923 | 0,7017 | 0,7109 | 0,7199 |
| 1,1 | |||||
| 1,2 | |||||
| 1,3 | |||||
| 1,4 | |||||
| 1,5 | |||||
| 1,6 | |||||
| 1,7 | |||||
| 1,8 | |||||
| 1,9 | |||||
| 2,0 | 0,9545 | 0,9566 | 0,9586 | 0,9606 | 0,9625 |
| 2,1 | |||||
| 2,2 | |||||
| 2,3 | |||||
| 2,4 | |||||
| 2,5 | |||||
| 2,6 | |||||
| 2,7 | |||||
| 2,8 | |||||
| 2,9 | |||||
| 3,0 | 0,9973 | 0,9975 | 0,9976 | 0,9978 | 0,9979 |
| 3,1 | |||||
| 3,2 | |||||
| 3,3 | |||||
| 3,4 | |||||
| 3,5 | |||||
| 3,6 |
 2015-04-08
2015-04-08 560
560








