2015-04-08
1608
При оценке достоверности средних или относительных величин руководствуются следующим правилом:средняя арифметическая или относительная величина при числе наблюдений в выборочной совокупности 30 и более должны превышать свою ошибку не менее чем в 2 раза.
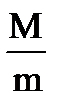> 2 или 
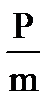> 2
В рассматриваемых примерах средняя арифметическая, характеризующая рост восьмилетних мальчиков и показатель „индекс здоровья” превышают свои ошибки соответственно:
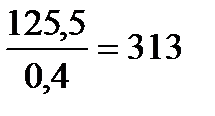раз,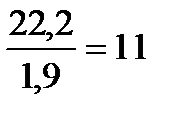 
раз, что соответствует высокой степени их статистической достоверности с вероятностью более чем 99,7 %.
Высказанное положение вытекает из теории «вероятности», под которой понимается числовая мера объективной возможности появления случайного события.
Вероятность - число, которое находится между 0 и 1, или между 0% и 100%. Математиками определено, что той или иной вероятности, выраженной в процентах, соответствует определенное значение критерия t Стьюдента.
Так, например, вероятности равной Р = 68,3% соответствует t= 1,0,
вероятности равной Р = 95,5 % соответствует t = 2,0
вероятности равной Р = 99,7 % соответствует t = 3,0
В медико-биологических исследованиях событие является статистически достоверным, если вероятность его появления соответствует значению критерия t Стьюдента, равное 2.
Средняя ошибка позволяет не только оценить достоверность относительного показателя или средней величины, но и найти доверительные границы средней величины или относительного показателя в генеральной совокупности
М ген.= М выб. ± t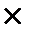 
m
Р ген. = Р выб. ± t 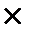m
Как уже было сказано, величина средней ошибки указывает, насколько средняя величина и относительный показатель выборочной совокупности отличаются от соответствующих величин в генеральной совокупности. Величина t*m является тем доверительным интервалом по отношению к средней или относительной величине, в котором с определенной степенью вероятности можно ожидать нахождение средней или относительной величины в генеральной совокупности.
