Средняя арифметическая

Одной из важнейших обобщающих характеристик вариаци­онного ряда является средняя величина признака (обычно обознача­ется буквой М). Существует несколько видов средних (сред­няя арифметическая – простая и взвешенная, средняя гармо­ническая, средняя квадратичная), но в практике биологических исследований наибольшее значение имеет средняя арифметиче­ская – величина, вокруг которой «концентрируются» варианты.

Общая формула для определения величины средней ариф­метической – это отношение суммы значений всех вариант (x_i) выборки к их числу (объему выборки, n):

.

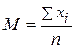В нашем примере с определением массы бурозубок средняя величина равна M = 9.298412698 г. При расчетах статистических параметров на ЭВМ следует помнить, что большое количество значащих цифр обычно не имеет никакого биологического смысла. Записывая такие статистические параметры, как средняя и стандартное отклонение, следует оставлять в лучшем случае на одну значащую цифру больше, чем имели значения вариант, а оценки ошибок – на две значащих цифры. Масса тела бурозубок колебалась от 7.3 до 11.9 г, отсюда средняя с учетом округления должна иметь вид M = 9.3 г.

Средняя арифметическая характеризует действие только систематических факторов, поскольку сумма случайных отклонений влево и вправо от средней в силу симметричности нормального распределения обращается в нуль. Поэтому модель варианты меняется: x_i = M ± x_случ.

В биологических исследованиях зачастую встречается ситуа­ция, когда требуется первичная статистическая обработка большого числа выборок, но необязательно с большой точностью. Это может понадобиться для предварительного рас­смотрения и оценки материала, в частности для оперативного выявления общих тенденций его изменчивости, с тем, чтобы в дальнейшем перейти к специальным методам статистического анализа. Для этих слу­чаев предложен простой экспресс-метод с использова­нием полученного для данной выборки размаха значений (Lim). В случае нормального распределения средняя арифметическая находится точно по центру (совпадает со значением медианы), т. е. левая и правая границы распределения находятся на одинаковом расстоянии от средней. Исходя из этих соображений, среднюю арифметическую можно рассчитать по формуле медианы:

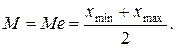
Для бурозубок эта средняя составит M = (7.3 + 11.9) / 2 = 9.6 г, что вполне соответствует первой точной оценке.

В случаях, когда необходимо объединить результаты расчетов по нескольким выборкам и на этой основе найти общую среднюю, характеризующую весь изученный материал, пользуются взвешенной средней, которая учитывает объемы частных выборок:

,

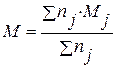где M_j – значение частной средней,

n_j – условные «веса» частного значения, объемы выборок.

Чтобы рассчитать среднюю взвешенную, необходимо значения всех частных средних арифметических помножить на свои «веса», все эти произведения сложить и сумму разде­лить на сумму весов (общий объем всех выборок). Пусть получены результаты определения средней величины выводка у рыжих полевок (экз./ самку) по месяцам: май 5.0, июнь 5.4, июль 6.2, август 6.0, сентябрь 4.5, причем известно число определений (самок) для каждого месяца: 22, 43, 103, 33 и 5. Взвешенная средняя арифметическая составит:

M = (5∙22 + 5.4∙43 + 6.2∙103 + 6∙33 + 4.5∙5) / (22 + 43 + 103 + 33 + 5) = 5.8.

Средняя, рассчитанная обычным спо­собом, оказалась заниженной:

М = (5 + 5.4 + 6.2 + 6 + 4.5) / 5 = 5.4.

В число прочих констант вариационного ряда входит медиана (Me) – значение, делящее размах выборки пополам, и мода (Mo) – класс (или значение), представленный наибольшим числом вариант.