Свойства электромагнитных волн

Следствием теории Максвелла, подтвержденным опытом, является поперечность электромагнитных волн: в электромагнитной волне колебания векторов напряженностей переменного электрического поля 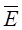и переменного магнитного поля 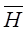взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору 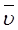скорости распространения волны (рис. 1).

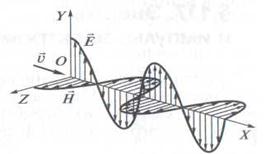
Рис. 1

На рисунке показана моментальная «фотография» плоской электромагнитной волны. Векторы 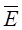, 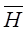и 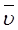образуют правовинтовую систему: направление распространения электромагнитной волны совпадает с поступательным движением острия винта, головка которого вращается по направлению кратчайшего поворота от вектора 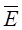к вектору 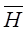(смотреть надо вдоль направления распространения волны).

Из уравнений Максвелла следует также, что в электромагнитной волне векторы 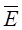и 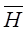всегда колеблются в одинаковых фазах, причем мгновенные значения Е и Н в любой точке связаны соотношением

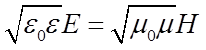(3)

Следовательно, Е и Н одновременно достигают максимума, одновременно обращаются в нуль и т.д.

От волновых уравнений (1) можно перейти к уравнениям вида

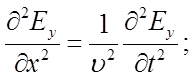(4)

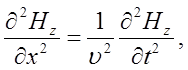(5)

Где индексы у и z при Е и Н подчеркивают лишь то, что векторы 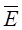и 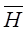направлены вдоль взаимно перпендикулярных осей ОY и OZ (см. рис.1). Уравнениям (4), (5) удовлетворяют, в частности, плоские монохроматические электромагнитные волны (электромагнитные волны одной строго определенной частоты), описываемые уравнениями:

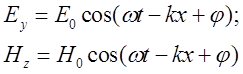(6)

Где 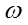- циклическая частота; 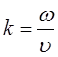- волновое число; 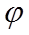- начальные фазы колебаний в точках с координатой Х=0.