2015-04-12
6134
Из формулы, записанной в виде
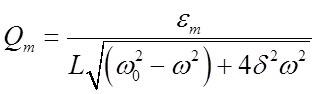(25)
Следует, что при некоторой определенной для данного колебательного контура частоте амплитуда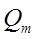 
достигает максимального значения.
Для определения резонансной частоты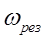 
- частоты, при которой амплитуда заряда достигнет максимума, нужно найти максимум функции (25) или, что то же самое, минимум подкоренного выражения. Продифференцировав подкоренное выражение по 
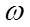и приравняв его нулю, получим, что резонансная частота для заряда равна
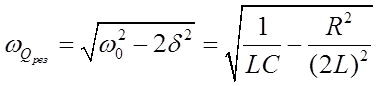(26)
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты внешней ЭДС к частоте, равной или близкой собственной частоте колебательного контура, называют электрическим резонансом. Подставив формулу (26) в выражение (25), получим
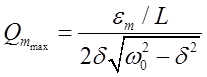(27)
На рис. 3 приведено семейство резонансных кривых – зависимостей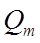 
от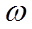 
при различных коэффициентах затухания 
.
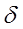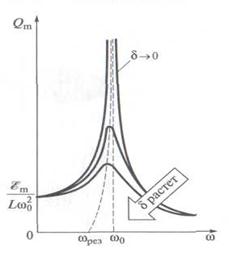
Из рисунка и формулы (27) следует, что с уменьшением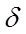 
максимумы кривых лежат выше и правее. При 
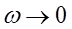все кривые приходят к так называемому статическому отклонению 
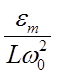. Если 
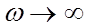, то все кривые асимптотически стремятся к нулю.
Резонансная частота для силы тока совпадает с собственной частотой контура:
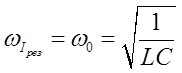
Амплитуда силы тока максимальна при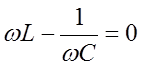 
. Семейство резонансных кривых для силы тока в контуре 
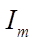от частоты 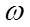внешней ЭДС при различных коэффициентах затухания 
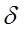- представлено на рис.4.
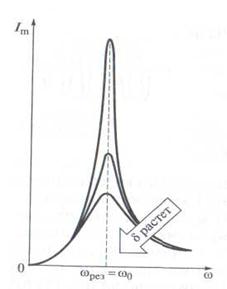
Рис. 4
Амплитуда силы тока максимальна пр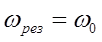и 
и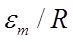 
. Чем больше коэффициент затухания 
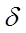, тем ниже максимум резонансной кривой.
ВОЛНЫ
