Парная регрессия и корреляция в эконометрических исследованиях

Регрессион-ый анализ позволяет проанализировать и оценить связи м/д зависимой (У) и не зависимой (Х1,Х2) переменными.Зависимую переменную наз-ют результ-ым признаком. Термин ввел Лор Ф.Гальтон. Модель регресии у=α+βх+Е,где (α+βх)-не случ.переменные,Е-случ-ая;х-не зависимая переменная, α,β-постоянные числа. Главная задача регрессион.анализа-подобрать такие значения а и b параметров α и β,чтобы построенная модель как можно точнее описала реальные данные.Причины отклонения прямой:ошибкиизмерения,не включение объясн.переменных.не правильный выбор вида зависимости.

Метод наименьших квадратов применяется для разл-ого вида зависимости,наиболее распространенная у= α+βхi+Еi, i=1,2,3..n Метод наименьших квадратов позволяет получить такие оценки а и b, при которых симма квадратов отклонения Е факт.значений признака уiявл-ся минимальной. Если найти миним.функции,приравнять каждую производную к нулю,преобразовать то получим сист-му уравнений по методу наименьших квад-ов 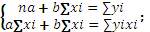b-выборочный коэф-т,а-указывает на значение результативного признака.Одним из показателей качества построеннгоуравненич регрессии явл-сякоэф-т детерминации 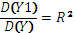,но для определения коэф-та детерминации нужно определить коэф.кореляции 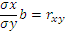. Коэф-т кореляции варьирует от 0до 1 без учета знака. Чем ближе к 1,тем связь более стабильна между х и у. Коэ-т детермин. Варьирует от 0 до 100 в %. Качество модели проводят по F-критерию Фишера:предполагается,что коэф.регрессии=0,т.е. х и у не зависимы.